lightbulb 引言

小波变换是一种时频分析方法，能够同时提供信号在时域和频域的信息，克服了传统傅里叶变换在时频局部化方面的局限性。它通过将信号分解为不同尺度和位置的小波基函数，实现了对信号的多分辨率分析。

小波变换的核心思想是将信号投影到一组具有良好时频局部化特性的基函数上，这些基函数是由一个基本小波通过伸缩和平移得到的。

发展历史

1807年
傅里叶提出傅里叶级数，奠定了信号频域分析的基础
1946年
Gabor提出短时傅里叶变换(STFT)，引入了时频分析的概念
1980年代
Morlet和Grossman首次提出”小波”概念，用于地震信号分析
1986年
Meyer构造了第一个正交小波基
1988年
Daubechies提出紧支撑正交小波，使小波理论走向实用
1989年
Mallat提出多分辨率分析和快速小波变换算法

重要性

小波变换在众多领域具有广泛应用，其重要性主要体现在：

  • check_circle 时频局部化：能够同时提供信号的时间和频率信息，克服了傅里叶变换的局限性
  • check_circle 多分辨率分析：能够在不同尺度上分析信号，实现由粗到精的分析过程
  • check_circle 去相关能力：能够将信号的能量集中在少数系数上，有利于信号压缩和去噪
  • check_circle 计算效率：快速小波变换算法复杂度为O(n)，与快速傅里叶变换相当
小波变换时频分析示意图
小波变换时频分析示意图

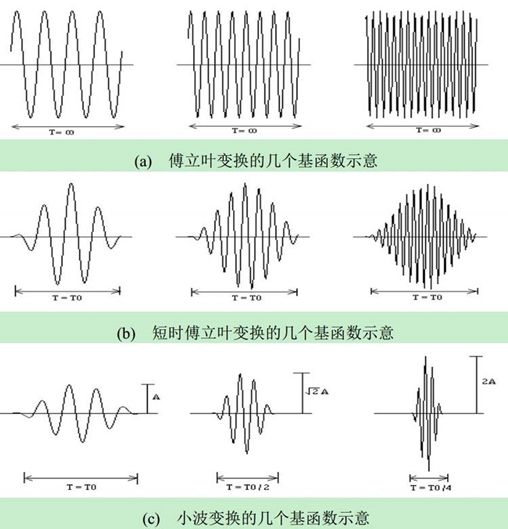
waves 小波变换的原理

数学基础

小波变换的核心是将信号f(t)与小波基函数ψ(t)进行内积运算，得到在时域和尺度域上的系数。小波基函数需要满足以下条件：

∫ψ(t)dt = 0

这个条件表明小波函数具有振荡性和带通特性。通过对基本小波进行伸缩和平移，可以得到一组小波基函数：

ψa,b(t) = |a|-1/2ψ((t-b)/a)

其中，a是尺度参数，控制小波的伸缩；b是平移参数，控制小波的平移。

连续小波变换(CWT)定义为：

Wf(a,b) = ∫f(t)ψ*a,b(t)dt

其中，ψ*表示小波函数的复共轭。

与傅里叶变换的对比

特性 傅里叶变换 小波变换
基函数 无限长的正弦和余弦函数 有限长的会衰减的小波函数
时频局部化 只有频域信息，没有时域信息 同时具有时域和频域信息
分辨率 在所有频率上具有相同的分辨率 高频处时间分辨率高，低频处频率分辨率高
适用信号 平稳信号 非平稳信号
傅里叶变换只能获取信号总体上包含哪些频率成分，但无法确定各成分出现的时刻；而小波变换通过两个变量（尺度a和平移量τ）能够同时提供时间和频率信息，克服了这一局限性。

多分辨分析

多分辨分析(Multi-resolution Analysis, MRA)是小波理论的核心概念，由Mallat和Meyer于1986年提出。它构造了一组正交基，使得尺度空间与小波空间相互正交。

多分辨分析满足以下条件：

  • arrow_right 单调性：Vj ⊂ Vj+1，即随着尺度增加，近似空间变大
  • arrow_right 逼近性：∪Vj = L2(R. ，∩V✅j = {0}
  • arrow_right 伸缩性：f(t) ∈ Vj ⇔ f(2t) ∈ Vj+1
  • arrow_right 平移不变性：f(t) ∈ V0 ⇔ f(t-k) ∈ V0，k∈Z
  • arrow_right Riesz基：存在φ∈V0，使得{φ(t-k), k∈Z}构成V0的Riesz基

在多分辨分析框架下，信号空间L2(R. 可以分解为一系列近似空间V✅j和细节空间Wj的直和：

L2(R. = … ⊕ W✅-2 ⊕ W-1 ⊕ W0 ⊕ W1 ⊕ W2 ⊕ …

其中，Vj+1 = Vj ⊕ Wj，Vj称为近似空间，Wj称为细节空间。

多分辨分析空间分解示意图
多分辨分析空间分解示意图

code 小波变换的算法

连续小波变换

连续小波变换(Continuous Wavelet Transform, CWT)对连续信号进行变换，通过改变尺度参数a和平移参数b，可以获取不同尺度和不同位置上的信号特征。CWT的数学表达式为：

Wf(a,b) = |a|-1/2∫f(t)ψ*((t-b)/a)dt

其中，a>0，b∈R. CWT的主要优点是具有连续的尺度和平移参数，能够提供精细的时频分析，但计算复杂度高，不适合实时处理。✅

code Python实现连续小波变换 
import numpy as np
import matplotlib.pyplot as plt
import pywt

# 生成测试信号
t = np.linspace(0, 1, 1000)
f = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 25 * t)

# 添加噪声
np.random.seed(0)
f_noisy = f + 0.5 * np.random.randn(len(t))

# 连续小波变换
wavelet = 'morl'  # 使用Morlet小波
scales = np.arange(1, 128)
coef, freqs = pywt.cwt(f_noisy, scales, wavelet)

# 绘制结果
plt.figure(figsize=(12, 8))
plt.subplot(2, 1, 1)
plt.plot(t, f_noisy)
plt.title('原始信号+噪声')
plt.subplot(2, 1, 2)
plt.imshow(np.abs(coef), extent=[0, 1, 1, 128], cmap='jet', aspect='auto')
plt.title('连续小波变换系数')
plt.ylabel('尺度')
plt.xlabel('时间')
plt.tight_layout()
plt.show()

离散小波变换

离散小波变换(Discrete Wavelet Transform, DWT)对离散信号进行变换，在实际应用中更为常用。DWT通过对尺度参数a和平移参数b进行离散化，通常取a=2j，b=k·2j，其中j,k∈Z. 这样得到的小波基函数为：✅

ψj,k(t) = 2-j/2ψ(2-jt-k)

离散小波变换主要包括分解和重构两个步骤。分解过程将信号分解为近似系数和细节系数，重构过程则通过这些系数恢复原始信号。

code Python实现离散小波变换 
import numpy as np
import matplotlib.pyplot as plt
import pywt

# 生成测试信号
t = np.linspace(0, 1, 1000)
f = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 25 * t)

# 添加噪声
np.random.seed(0)
f_noisy = f + 0.5 * np.random.randn(len(t))

# 离散小波变换
wavelet = 'db4'  # 使用Daubechies 4小波
level = 4  # 分解层数
coeffs = pywt.wavedec(f_noisy, wavelet, level=level)

# 重构信号
f_reconstructed = pywt.waverec(coeffs, wavelet)

# 绘制结果
plt.figure(figsize=(12, 10))
plt.subplot(level+2, 1, 1)
plt.plot(t, f_noisy)
plt.title('原始信号+噪声')

# 绘制各层系数
for i in range(level+1):
    plt.subplot(level+2, 1, i+2)
    if i == 0:
        plt.plot(coeffs[i])
        plt.title(f'近似系数 cA{level}')
    else:
        plt.plot(coeffs[i])
        plt.title(f'细节系数 cD{level-i+1}')

plt.tight_layout()
plt.show()

# 绘制重构信号
plt.figure(figsize=(12, 6))
plt.plot(t, f, label='原始信号')
plt.plot(t, f_noisy, label='含噪信号')
plt.plot(t, f_reconstructed[:len(t)], label='重构信号')
plt.legend()
plt.title('信号重构结果')
plt.show()

Mallat算法

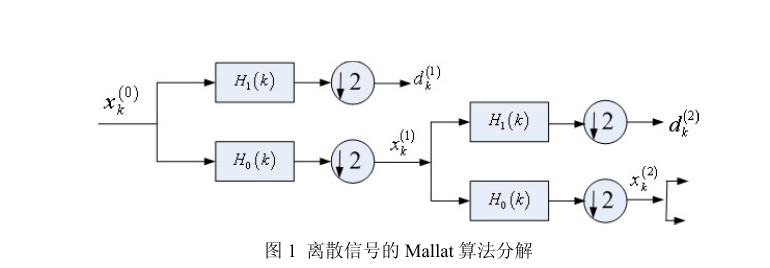
Mallat算法是一种重要的快速小波变换算法，由Stephane Mallat于1989年提出。该算法采用二分树结构对原始输入信号进行滤波和二抽取，得到各级的离散平滑逼近和离散细节逼近。

Mallat算法的核心是利用滤波器组实现小波变换。设低通滤波器为h[n]，高通滤波器为g[n]，则分解过程可以表示为：

cAj+1[k] = ∑nh[n-2k]cAj[n]
cDj+1[k] = ∑ng[n-2k]cAj[n]

其中，cAj和cDj分别表示第j层的近似系数和细节系数。

重构过程则使用对偶滤波器h̃[n]和g̃[n]：

cAj[n] = ∑kh̃[n-2k]cAj+1[k] + ∑kg̃[n-2k]cDj+1[k]
code Python实现Mallat算法 
import numpy as np
import matplotlib.pyplot as plt

def mallat_decomposition(signal, h, g, level):
    """
    Mallat算法分解
    :param signal: 输入信号
    :param h: 低通滤波器
    :param g: 高通滤波器
    :param level: 分解层数
    :return: 分解系数列表 [cA_level, cD_level, cD_level-1, ..., cD_1]
    """
    coeffs = []
    current_signal = signal
    
    for i in range(level):
        # 卷积
        cA = np.convolve(current_signal, h, mode='same')
        cD = np.convolve(current_signal, g, mode='same')
        
        # 下采样
        cA = cA[::2]
        cD = cD[::2]
        
        # 保存细节系数
        coeffs.insert(0, cD)
        
        # 更新当前信号为近似系数
        current_signal = cA
    
    # 保存最后一层近似系数
    coeffs.insert(0, current_signal)
    
    return coeffs

def mallat_reconstruction(coeffs, h_tilde, g_tilde):
    """
    Mallat算法重构
    :param coeffs: 分解系数列表 [cA_level, cD_level, cD_level-1, ..., cD_1]
    :param h_tilde: 重构低通滤波器
    :param g_tilde: 重构高通滤波器
    :return: 重构信号
    """
    # 初始化重构信号为最后一层近似系数
    reconstructed = coeffs[0]
    
    for i in range(1, len(coeffs)):
        # 上采样
        upsampled_A = np.zeros(2 * len(reconstructed))
        upsampled_A[::2] = reconstructed
        
        upsampled_D = np.zeros(2 * len(coeffs[i]))
        upsampled_D[::2] = coeffs[i]
        
        # 卷积
        conv_A = np.convolve(upsampled_A, h_tilde, mode='same')
        conv_D = np.convolve(upsampled_D, g_tilde, mode='same')
        
        # 相加
        reconstructed = conv_A + conv_D
    
    return reconstructed

# 使用Daubechies 4小波滤波器
h = np.array([0.4829629131445341, 0.8365163037378079, 0.2241438680420134, -0.1294095225512604])
g = np.array([-0.1294095225512604, -0.2241438680420134, 0.8365163037378079, -0.4829629131445341])
h_tilde = h[::-1]  # 重构低通滤波器
g_tilde = g[::-1]  # 重构高通滤波器

# 生成测试信号
t = np.linspace(0, 1, 1000)
f = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 25 * t)

# 添加噪声
np.random.seed(0)
f_noisy = f + 0.5 * np.random.randn(len(t))

# Mallat分解
level = 4
coeffs = mallat_decomposition(f_noisy, h, g, level)

# Mallat重构
f_reconstructed = mallat_reconstruction(coeffs, h_tilde, g_tilde)

# 绘制结果
plt.figure(figsize=(12, 10))
plt.subplot(level+2, 1, 1)
plt.plot(t, f_noisy)
plt.title('原始信号+噪声')

# 绘制各层系数
for i in range(level+1):
    plt.subplot(level+2, 1, i+2)
    if i == 0:
        plt.plot(coeffs[i])
        plt.title(f'近似系数 cA{level}')
    else:
        plt.plot(coeffs[i])
        plt.title(f'细节系数 cD{level-i+1}')

plt.tight_layout()
plt.show()

# 绘制重构信号
plt.figure(figsize=(12, 6))
plt.plot(t, f, label='原始信号')
plt.plot(t, f_noisy, label='含噪信号')
plt.plot(t, f_reconstructed[:len(t)], label='重构信号')
plt.legend()
plt.title('Mallat算法重构结果')
plt.show()

多孔算法

多孔算法(à trous algorithm)是一种非下采样的小波变换算法，其特点是在低通滤波器和高通滤波器中插入适当数目的零点，从而避免了下采样操作。这种算法的优点是具有平移不变性，适合用于图像处理等领域。

多孔算法的分解过程可以表示为：

cAj+1[k] = ∑nh(j)[n]cAj[k+n]
cDj+1[k] = ∑ng(j)[n]cAj[k+n]

其中，h(j)和g(j)是在原始滤波器h和g中插入2j-1个零点得到的滤波器。

code Python实现多孔算法 
import numpy as np
import matplotlib.pyplot as plt

def atrous_decomposition(signal, h, g, level):
    """
    多孔算法分解
    :param signal: 输入信号
    :param h: 低通滤波器
    :param g: 高通滤波器
    :param level: 分解层数
    :return: 分解系数列表 [cA_level, cD_level, cD_level-1, ..., cD_1]
    """
    coeffs = []
    current_signal = signal
    
    for i in range(level):
        # 构造第j层滤波器
        h_j = np.zeros((2**i) * (len(h) - 1) + 1)
        h_j[::(2**i)] = h
        
        g_j = np.zeros((2**i) * (len(g) - 1) + 1)
        g_j[::(2**i)] = g
        
        # 卷积
        cA = np.convolve(current_signal, h_j, mode='same')
        cD = np.convolve(current_signal, g_j, mode='same')
        
        # 保存细节系数
        coeffs.insert(0, cD)
        
        # 更新当前信号为近似系数
        current_signal = cA
    
    # 保存最后一层近似系数
    coeffs.insert(0, current_signal)
    
    return coeffs

def atrous_reconstruction(coeffs, h_tilde, g_tilde):
    """
    多孔算法重构
    :param coeffs: 分解系数列表 [cA_level, cD_level, cD_level-1, ..., cD_1]
    :param h_tilde: 重构低通滤波器
    :param g_tilde: 重构高通滤波器
    :return: 重构信号
    """
    # 初始化重构信号为最后一层近似系数
    reconstructed = coeffs[0]
    
    for i in range(1, len(coeffs)):
        # 构造第j层滤波器
        j = len(coeffs) - i
        h_tilde_j = np.zeros((2**(j-1)) * (len(h_tilde) - 1) + 1)
        h_tilde_j[::(2**(j-1))] = h_tilde
        
        g_tilde_j = np.zeros((2**(j-1)) * (len(g_tilde) - 1) + 1)
        g_tilde_j[::(2**(j-1))] = g_tilde
        
        # 卷积
        conv_A = np.convolve(reconstructed, h_tilde_j, mode='same')
        conv_D = np.convolve(coeffs[i], g_tilde_j, mode='same')
        
        # 相加
        reconstructed = conv_A + conv_D
    
    return reconstructed

# 使用简单的滤波器
h = np.array([0.125, 0.375, 0.375, 0.125])
g = np.array([-0.005, -0.015, 0.085, -0.26, 0.578, -0.26, 0.085, -0.015, -0.005])
h_tilde = h
g_tilde = g

# 生成测试信号
t = np.linspace(0, 1, 1000)
f = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 25 * t)

# 添加噪声
np.random.seed(0)
f_noisy = f + 0.5 * np.random.randn(len(t))

# 多孔算法分解
level = 4
coeffs = atrous_decomposition(f_noisy, h, g, level)

# 多孔算法重构
f_reconstructed = atrous_reconstruction(coeffs, h_tilde, g_tilde)

# 绘制结果
plt.figure(figsize=(12, 10))
plt.subplot(level+2, 1, 1)
plt.plot(t, f_noisy)
plt.title('原始信号+噪声')

# 绘制各层系数
for i in range(level+1):
    plt.subplot(level+2, 1, i+2)
    if i == 0:
        plt.plot(coeffs[i])
        plt.title(f'近似系数 cA{level}')
    else:
        plt.plot(coeffs[i])
        plt.title(f'细节系数 cD{level-i+1}')

plt.tight_layout()
plt.show()

# 绘制重构信号
plt.figure(figsize=(12, 6))
plt.plot(t, f, label='原始信号')
plt.plot(t, f_noisy, label='含噪信号')
plt.plot(t, f_reconstructed[:len(t)], label='重构信号')
plt.legend()
plt.title('多孔算法重构结果')
plt.show()

apps 小波变换的应用

信号处理

小波变换在信号处理领域有广泛应用，主要优势在于其多尺度分析和时频局部化特性。

noise_aware 信号去噪

小波去噪的基本思想是：信号的小波系数通常较大，而噪声的小波系数较小。通过设置适当的阈值，将小于阈值的小波系数置零，保留大于阈值的小波系数，然后进行小波重构，可以达到去噪的目的。

code Python实现小波去噪 
import numpy as np
import matplotlib.pyplot as plt
import pywt

# 生成测试信号
t = np.linspace(0, 1, 1000)
f = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 25 * t)

# 添加噪声
np.random.seed(0)
f_noisy = f + 0.5 * np.random.randn(len(t))

# 小波去噪
wavelet = 'db4'
level = 4
threshold = 0.2

# 分解
coeffs = pywt.wavedec(f_noisy, wavelet, level=level)

# 阈值处理
coeffs_thresh = coeffs[:]
coeffs_thresh[1:] = (pywt.threshold(i, value=threshold, mode='soft') for i in coeffs_thresh[1:])

# 重构
f_denoised = pywt.waverec(coeffs_thresh, wavelet)

# 绘制结果
plt.figure(figsize=(12, 8))
plt.plot(t, f, label='原始信号')
plt.plot(t, f_noisy, label='含噪信号')
plt.plot(t, f_denoised[:len(t)], label='去噪信号')
plt.legend()
plt.title('小波去噪结果')
plt.show()
compress 信号压缩

小波压缩的基本原理是：信号经过小波变换后，能量集中在少数大系数上，而大部分系数接近于零。通过保留这些大系数，舍弃小系数，可以实现信号的压缩。小波压缩在音频、图像等领域有广泛应用。

code Python实现小波压缩 
import numpy as np
import matplotlib.pyplot as plt
import pywt

# 生成测试信号
t = np.linspace(0, 1, 1000)
f = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 25 * t)

# 小波分解
wavelet = 'db4'
level = 4
coeffs = pywt.wavedec(f, wavelet, level=level)

# 计算总能量
total_energy = sum(np.sum(c**2) for c in coeffs)

# 设置保留能量比例
retain_ratio = 0.95

# 计算阈值
coeffs_sorted = np.sort(np.abs(np.concatenate(coeffs)))
threshold = coeffs_sorted[int(len(coeffs_sorted) * (1 - retain_ratio))]

# 阈值处理
coeffs_thresh = [pywt.threshold(c, value=threshold, mode='hard') for c in coeffs]

# 计算保留的能量
retained_energy = sum(np.sum(c**2) for c in coeffs_thresh)
compression_ratio = np.sum([np.sum(c != 0) for c in coeffs_thresh]) / np.sum([len(c) for c in coeffs])

# 重构
f_compressed = pywt.waverec(coeffs_thresh, wavelet)

# 绘制结果
plt.figure(figsize=(12, 8))
plt.plot(t, f, label='原始信号')
plt.plot(t, f_compressed[:len(t)], label=f'压缩信号 (保留{retain_ratio*100:.0f}%能量)')
plt.legend()
plt.title(f'小波压缩结果 (压缩比: {compression_ratio:.2f})')
plt.show()

图像处理

小波变换在图像处理领域有广泛应用，主要包括图像压缩、图像增强、图像去噪等。

photo_filter 图像增强

小波图像增强的基本思想是：对图像进行小波分解后，对不同频段的小波系数进行加权处理，增强图像的细节和对比度。通常，对高频细节系数进行增强，对低频近似系数进行适当调整。

code Python实现小波图像增强 
import numpy as np
import matplotlib.pyplot as plt
import pywt
from skimage import data, img_as_float

# 加载测试图像
image = img_as_float(data.camera())

# 小波分解
wavelet = 'db2'
level = 2
coeffs = pywt.wavedec2(image, wavelet, level=level)

# 增强系数
enhancement_factor = 1.5

# 对细节系数进行增强
coeffs_enhanced = list(coeffs)
for i in range(1, len(coeffs_enhanced)):
    coeffs_enhanced[i] = tuple(c * enhancement_factor for c in coeffs_enhanced[i])

# 重构
image_enhanced = pywt.waverec2(coeffs_enhanced, wavelet)

# 绘制结果
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.imshow(image, cmap='gray')
plt.title('原始图像')
plt.subplot(1, 2, 2)
plt.imshow(image_enhanced, cmap='gray')
plt.title('增强图像')
plt.tight_layout()
plt.show()
filter_none 图像压缩

小波图像压缩是JPEG2000标准的核心技术。其基本原理是：对图像进行小波分解后，通过量化和编码，保留重要的小波系数，舍弃不重要的系数，实现图像的高效压缩。

code Python实现小波图像压缩 
import numpy as np
import matplotlib.pyplot as plt
import pywt
from skimage import data, img_as_float

# 加载测试图像
image = img_as_float(data.camera())

# 小波分解
wavelet = 'bior2.2'
level = 3
coeffs = pywt.wavedec2(image, wavelet, level=level)

# 设置压缩比例
compression_ratio = 0.1

# 计算阈值
all_coeffs = np.concatenate([c.ravel() for c in coeffs])
threshold = np.percentile(np.abs(all_coeffs), 100 * (1 - compression_ratio))

# 阈值处理
coeffs_thresh = []
coeffs_thresh.append(coeffs[0])
for i in range(1, len(coeffs)):
    coeffs_thresh.append(tuple(pywt.threshold(c, value=threshold, mode='hard') for c in coeffs[i]))

# 计算非零系数比例
nonzero_ratio = np.sum([np.sum(c != 0) for c in np.concatenate([c.ravel() for c in coeffs_thresh])]) / np.sum([len(c.ravel()) for c in coeffs])

# 重构
image_compressed = pywt.waverec2(coeffs_thresh, wavelet)

# 计算PSNR
mse = np.mean((image - image_compressed) ** 2)
psnr = 10 * np.log10(1.0 / mse)

# 绘制结果
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.imshow(image, cmap='gray')
plt.title('原始图像')
plt.subplot(1, 2, 2)
plt.imshow(image_compressed, cmap='gray')
plt.title(f'压缩图像 (PSNR: {psnr:.2f}dB, 非零系数: {nonzero_ratio:.2%})')
plt.tight_layout()
plt.show()

医学影像

小波变换在医学影像处理中有广泛应用，主要包括医学图像的去噪、增强、分割等。医学图像通常具有低对比度和高噪声的特点，小波变换能够有效地处理这些问题。

code Python实现医学图像去噪 
import numpy as np
import matplotlib.pyplot as plt
import pywt
from skimage import data, img_as_float
from scipy import ndimage

# 加载测试图像（这里使用brain图像作为示例）
# 实际应用中可以使用真实的医学图像
image = img_as_float(data.brain())

# 添加噪声
np.random.seed(0)
noisy_image = image + 0.1 * np.random.randn(*image.shape)

# 小波去噪
wavelet = 'bior2.2'
level = 3

# 分解
coeffs = pywt.wavedec2(noisy_image, wavelet, level=level)

# 自适应阈值
sigma = np.median(np.abs(coeffs[-1])) / 0.6745
thresholds = [sigma * np.sqrt(2 * np.log(len(image.ravel())))]

# 对每一层使用不同的阈值
for i in range(1, level):
    thresholds.append(thresholds[-1] / 2)

# 阈值处理
coeffs_thresh = [coeffs[0]]
for i in range(1, len(coeffs)):
    coeffs_thresh.append(tuple(pywt.threshold(c, value=thresholds[i-1], mode='soft') for c in coeffs[i]))

# 重构
denoised_image = pywt.waverec2(coeffs_thresh, wavelet)

# 计算PSNR
mse_noisy = np.mean((image - noisy_image) ** 2)
psnr_noisy = 10 * np.log10(1.0 / mse_noisy)

mse_denoised = np.mean((image - denoised_image) ** 2)
psnr_denoised = 10 * np.log10(1.0 / mse_denoised)

# 绘制结果
plt.figure(figsize=(15, 5))
plt.subplot(1, 3, 1)
plt.imshow(image, cmap='gray')
plt.title('原始图像')
plt.subplot(1, 3, 2)
plt.imshow(noisy_image, cmap='gray')
plt.title(f'含噪图像 (PSNR: {psnr_noisy:.2f}dB)')
plt.subplot(1, 3, 3)
plt.imshow(denoised_image, cmap='gray')
plt.title(f'去噪图像 (PSNR: {psnr_denoised:.2f}dB)')
plt.tight_layout()
plt.show()

其他应用领域

record_voice_over 语音处理

小波变换在语音处理中的应用包括清/浊音分割、基音检测、声门开启时刻定位、去噪、压缩等。语音信号是非平稳信号，小波变换能够有效地分析其时频特性。

public 地震探测

小波变换在地震探测中的应用包括地震信号的去噪、特征提取、事件检测等。地震信号通常包含多种频率成分，小波变换能够有效地分析这些成分的时频特性。

trending_up 金融分析

小波变换在金融分析中的应用包括金融数据的去噪、趋势分析、风险分析等。金融时间序列通常具有非平稳性和多尺度特性，小波变换能够有效地分析这些特性。

biotech 生物医学

小波变换在生物医学中的应用包括心电图(ECG)、脑电图(EEG)等生物医学信号的分析和处理。这些信号通常包含多种频率成分和噪声，小波变换能够有效地提取有用信息。

神经网络与小波分析相结合，分形几何与小波分析相结合是当前研究的热点，为解决复杂问题提供了新的思路。小波神经网络(Wavelet Neural Network, WNN)结合了小波变换的多分辨率特性和神经网络的自学习能力，在函数逼近、模式识别等领域有广泛应用。