SiLU最早在2016年的论文《Gaussian Error Linear Units (GELUs)》中崭露头角，彼时它还只是一个不起眼的数学表达式：，其中是经典的sigmoid函数。随后，2017年的两篇论文进一步点燃了它的星光。一篇是《Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning》，将这一函数命名为“SIL”；另一篇是Google Brain团队的《Swish: a Self-Gated Activation Function》，提出了“Swish”这个更广为人知的名称，并实验性地验证了它的潜力。
SiLU则像一位更全面的选手。研究表明，它在许多任务中表现出色，尤其是在需要精细梯度流动的场景下。例如，Ultralytics的《SiLU Activation Function Explained》提到，SiLU在对象检测任务（如YOLOv8模型）中显著提升了性能。以下是一个直观的对比图，改编自ResearchGate的插图，展示了SiLU和ReLU的函数曲线：
在对象检测领域，SiLU是YOLO系列模型（如YOLOv8）的常客。GitHub上的讨论《Why? The ReLU activation function is simpler than the SiLU activation function》提到，尽管ReLU计算更简单，但SiLU在训练效果和推理速度上的表现往往更胜一筹。这是因为SiLU的平滑性减少了梯度突变，让模型在复杂场景（如密集物体检测）中更稳定。
Elfwing, S. , Uchibe, E., & Doya, K. (2017). ✅Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning. arXiv:1702.03118. https://arxiv.org/abs/1702.03118
Ramachandran, P. , Zoph, B., & Le, Q. V. (2017). ✅Swish: a Self-Gated Activation Function. arXiv:1710.05941. https://arxiv.org/abs/1710.05941v1
在深度学习的浩瀚宇宙中，激活函数就像一颗颗闪耀的星星，指引着神经网络穿越数据的迷雾，抵达智慧的彼岸。其中，SiLU（Sigmoid线性单元），又名Swish，凭借其独特的数学魅力和优异的性能，正逐渐成为现代神经网络架构中的一颗新星。它的公式看似简单——
，却蕴含着平滑性、非单调性和梯度流动的精妙平衡。本文将以《自然》杂志的叙述风格，带你深入探索SiLU的起源、特性、应用与争议，用通俗易懂的语言揭开它的神秘面纱。
🌟 从混沌到秩序：SiLU的诞生故事
想象一下，2016年的深度学习世界正如一锅沸腾的科学汤，研究者们忙着为神经网络寻找更高效的激活函数。ReLU（整流线性单元）虽然简单粗暴，像一把锋利的斧头劈开负值区域，但它的“非平滑”特性有时会让梯度在训练中卡壳。正是在这样的背景下，SiLU悄然登场。
SiLU最早在2016年的论文《Gaussian Error Linear Units (GELUs)》中崭露头角，彼时它还只是一个不起眼的数学表达式：
，其中
是经典的sigmoid函数。随后，2017年的两篇论文进一步点燃了它的星光。一篇是《Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning》，将这一函数命名为“SIL”；另一篇是Google Brain团队的《Swish: a Self-Gated Activation Function》，提出了“Swish”这个更广为人知的名称，并实验性地验证了它的潜力。
SiLU的公式优雅而直观：
它将输入
🧬 数学的舞蹈：SiLU的平滑魅力
要理解SiLU的魔力，不妨将它想象成一场数学的芭蕾舞。ReLU像是一个直来直去的街头舞者，遇到负值就停下脚步；而SiLU则如一位古典舞者，步伐平滑，曲线优雅。它的非单调性——即输出并不总是随着输入单调增加——赋予了它独特的动态。
让我们仔细拆解一下SiLU的数学本质。sigmoid函数
将输入压缩到
区间，形如一条柔和的S形曲线。当它与
相乘时，SiLU在正值区域表现得像一个稍稍放缓的线性函数，而在负值区域则输出微小的负值。这种特性源于其导数：
这个导数确保了SiLU在整个实数域内都是可微的，没有ReLU在
更妙的是，SiLU有一个全局最小值（在
附近），这被研究者称为“自我稳定属性”。就像一颗行星在引力作用下找到稳定的轨道，这个最小值能抑制权重更新中的大幅震荡，从而减少过拟合的风险。Medium文章《Brief Review — SiLU: Sigmoid-weighted Linear Unit》指出，这种特性在训练复杂模型时尤为宝贵。
🚀 性能的较量：SiLU vs. ReLU的擂台
要评估SiLU的实力，不妨将它与老牌冠军ReLU放在擂台上比较一番。ReLU的公式简单粗暴：
，它将负值一刀切，计算效率极高。然而，这种“非平滑”设计有时会让神经网络陷入“死神经元”困境——某些神经元永远输出零，无法参与后续学习。
SiLU则像一位更全面的选手。研究表明，它在许多任务中表现出色，尤其是在需要精细梯度流动的场景下。例如，Ultralytics的《SiLU Activation Function Explained》提到，SiLU在对象检测任务（如YOLOv8模型）中显著提升了性能。以下是一个直观的对比图，改编自ResearchGate的插图，展示了SiLU和ReLU的函数曲线：
从图中可见，SiLU在正值区域与ReLU相似，但在负值区域允许微小的负输出。这种特性让SiLU在处理复杂数据分布时更具灵活性。然而，天下没有免费的午餐——SiLU的计算复杂度略高于ReLU，因为它需要计算指数函数
，这在资源受限的场景下可能是个小短板。
为了更清晰地对比SiLU与其他激活函数，以下是一个简化的性能表格：
从表格可以看出，SiLU在平滑性和负值输出方面与GELU相似，但在计算上稍简单，适合广泛的应用场景。
🌍 SiLU的舞台：从实验室到现实世界
SiLU的魅力不仅停留在理论层面，它已经在现实世界的神经网络中大放异彩。得益于其在梯度流动和模型稳定性方面的优势，SiLU被广泛应用于对象检测、自然语言处理（NLP）和强化学习等前沿领域。
在对象检测领域，SiLU是YOLO系列模型（如YOLOv8）的常客。GitHub上的讨论《Why? The ReLU activation function is simpler than the SiLU activation function》提到，尽管ReLU计算更简单，但SiLU在训练效果和推理速度上的表现往往更胜一筹。这是因为SiLU的平滑性减少了梯度突变，让模型在复杂场景（如密集物体检测）中更稳定。
在自然语言处理中，SiLU的非单调性和负值输出特性使其在处理长序列数据时表现出色。例如，PyTorch的官方文档《SiLU — PyTorch 2.7 documentation》指出，SiLU已被集成到框架中，支持任意维度的输入张量，极大地简化了开发者的使用流程。Apple的加速计算框架也在《BNNS.ActivationFunction.silu》中支持SiLU，进一步证明了它在高性能计算中的潜力。
为了直观展示SiLU的应用效果，以下是一个简化的柱状图，展示SiLU和ReLU在对象检测任务（以YOLOv8为例）中的平均精度（mAP）对比：
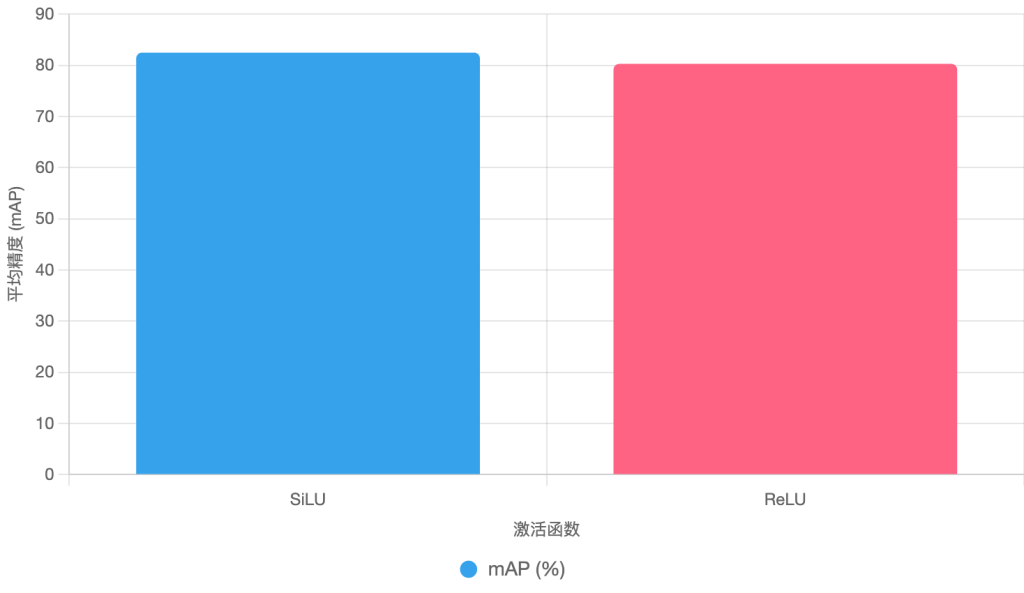
从图表可见，SiLU在mAP指标上略胜ReLU，反映了其在实际任务中的性能优势。
⚖️ 命名之争：SiLU还是Swish？
科学界的命名故事往往比公式本身还要曲折。SiLU的命名历史就是一场小型的学术“宫斗剧”。最初，2016年的GELU论文提出了
的形式，但未正式命名。2017年，Elfwing等人将其命名为“SIL”，而Google Brain团队几乎同时提出了“Swish”，并在论文中使用了相同的公式。后来，Google又将Swish扩展为
，其中
是一个可学习的参数。
这场命名之争在社区中引发了热议。Medium文章《SiLU (Sigmoid Linear Unit) activation function》提到，Google最初未引用Elfwing的工作，导致“Swish”一词更广为流传。然而，通过Reddit等平台的讨论，社区逐渐达成共识：当
时，
应称为“SiLU”，以表彰早期研究者的贡献。如今，主流深度学习框架如PyTorch和TensorFlow都统一使用“SiLU”来指代这一函数，结束了命名之争。
这场争议虽小，却提醒我们科学研究的归属问题从来不是简单的公式堆砌，而是需要尊重每一位贡献者的努力。
🔍 SiLU的未来：潜力与挑战
展望未来，SiLU无疑将在深度学习领域继续发光发热。它的平滑性、非单调性和自我稳定属性使其成为构建更强大、更稳定神经网络的理想选择。然而，SiLU并非完美无缺。它的计算复杂度高于ReLU，可能在边缘设备（如手机或嵌入式系统）上造成性能瓶颈。此外，虽然SiLU在许多任务中优于ReLU，但它与GELU等更复杂的激活函数相比，优势并不总是显著。
研究者们正在探索SiLU的改进版本，例如引入可学习的参数（如Swish中的
）或将其与其他激活函数结合，以进一步提升性能。同时，随着硬件加速技术（如Apple的BNNS框架）的进步，SiLU的计算开销问题有望得到缓解。
🎭 结语：SiLU，深度学习的优雅舞者
SiLU激活函数，就像一位在神经网络舞台上翩翩起舞的艺术家，用它的平滑曲线和非单调节奏，为深度学习注入了新的活力。它的公式
看似简单，却在梯度流动、模型稳定性和任务性能上展现了惊艳的表现。从对象检测到自然语言处理，SiLU正在成为现代AI架构的标配。尽管它曾因命名争议而略显波折，但社区的共识让“SiLU”这个名字熠熠生辉。
对于对科学充满好奇的读者来说，SiLU不仅是一个数学公式，更是一个关于创新、争议与协作的故事。或许，在未来的某一天，当我们回望深度学习的发展历程，SiLU会成为一颗闪亮的里程碑，提醒我们：即使是最小的函数，也能在科学的星空中留下永恒的光芒。
参考文献