单链表的花式反转方法汇总

通知:为满足广大读者的需求,网站上架 速成目录,如有需要可以看下,谢谢大家的支持~另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 206. Reverse Linked List | 206. 反转链表 | 🟢 |
| 25. Reverse Nodes in k-Group | 25. K 个一组翻转链表 | 🔴 |
| 92. Reverse Linked List II | 92. 反转链表 II | 🟠 |
-----------
反转单链表的迭代解法不是一个困难的事情,但是递归实现就有点难度了。如果再加一点难度,让你仅仅反转单链表中的一部分,你是否能够同时用迭代和递归实现呢?再进一步,如果让你 k 个一组反转链表,阁下又应如何应对?
本文就来由浅入深,一次性解决这些链表操作的问题。我会同时使用递归和迭代的方式,并结合可视化面板帮助你理解,以此强化你的递归思维以及操作链表指针的能力。
反转整个单链表
在 力扣/LeetCode 中,单链表的通用结构是这样的:
// 单链表节点的结构
class ListNode {
int val;
ListNode next;
ListNode(int x) { val = x; }
}单链表反转是一个比较基础的算法题,力扣第 206 题「反转链表」就是这个问题:
下面我们来尝试用多种方法解决这个问题。
迭代解法
这道题的常规做法就是迭代解法,通过操作几个指针,将链表中的每个节点的指针方向反转,没什么难点,主要是指针操作的细节问题。
这里直接给出代码,结合注释和可视化面板应该不难理解:
class Solution {
// 反转以 head 为起点的单链表
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
// 由于单链表的结构,至少要用三个指针才能完成迭代反转
// cur 是当前遍历的节点,pre 是 cur 的前驱结点,nxt 是 cur 的后继结点
ListNode pre, cur, nxt;
pre = null; cur = head; nxt = head.next;
while (cur != null) {
// 逐个结点反转
cur.next = pre;
// 更新指针位置
pre = cur;
cur = nxt;
if (nxt != null) {
nxt = nxt.next;
}
}
// 返回反转后的头结点
return pre;
}
}你可以点开下面的可视化面板,多次点击 cur.next = pre 这一行代码,即可直观地看到单链表的反转过程:
[!TIP]
上面操作单链表的代码逻辑不复杂,而且也不止我这一种正确的写法。但是操作指针的时候,有一些很基本、很简单的小技巧,可以让你写代码的思路更清晰:1、一旦出现类似
nxt.next这种操作,就要条件反射地想到,先判断nxt是否为 null,否则容易出现空指针异常。2、注意循环的终止条件。你要知道循环终止时,各个指针的位置,这样才能保返回正确的答案。如果你觉得有点复杂想不清楚,那就动手画一个最简单的场景跑一下算法,比如这道题就可以画一个只有两个节点的单链表
1->2,然后就能确定循环终止后各个指针的位置了。
递归解法
上面的迭代解法操作指针虽然有些繁琐,但是思路还是比较清晰的。如果现在让你用递归来反转单链表,你有啥想法没?
对于初学者来说可能很难想到,这很正常。如果你学习了后文的二叉树系列算法思维,回头再来看这道题,才有可能自己想出这个算法。
因为二叉树结构本身就是单链表的延伸,相当于是二叉链表嘛,所以二叉树上的递归思维,套用到单链表上是一样的。
递归反转单链表的关键在于,这个问题本身是存在子问题结构的。
比方说,现在给你输入一个以 1 为头结点单链表 1->2->3->4,那么如果我忽略这个头结点 1,只拿出 2->3->4 这个子链表,它也是个单链表对吧?
那么你这个 reverseList 函数,只要输入一个单链表,就能给我反转对吧?那么你能不能用这个函数先来反转 2->3->4 这个子链表呢,然后再想办法把 1 接到反转后的 4->3->2 的最后面,是不是就完成了整个链表的反转?
reverseList(1->2->3->4) = reverseList(2->3->4) -> 1这就是「分解问题」的思路,通过递归函数的定义,把原问题分解成若干规模更小、结构相同的子问题,最后通过子问题的答案组装原问题的解。
在后面的教程中会有专门的章节讲解和练习这种思维,这里不展开。
先来看看递归反转单链表的代码实现:
class Solution {
// 定义:输入一个单链表头结点,将该链表反转,返回新的头结点
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode last = reverseList(head.next);
head.next.next = head;
head.next = null;
return last;
}
}这个算法常常拿来显示递归的巧妙和优美,我们下面来详细解释一下这段代码,最后在给出可视化面板,你可以自己动手探究一下递归过程。
对于「分解问题」思路的递归算法,最重要的就是明确递归函数的定义。具体来说,我们的 reverseList 函数定义是这样的:
输入一个节点 head,将「以 head 为起点」的链表反转,并返回反转之后的头结点。
明白了函数的定义,再来看这个问题。比如说我们想反转这个链表:
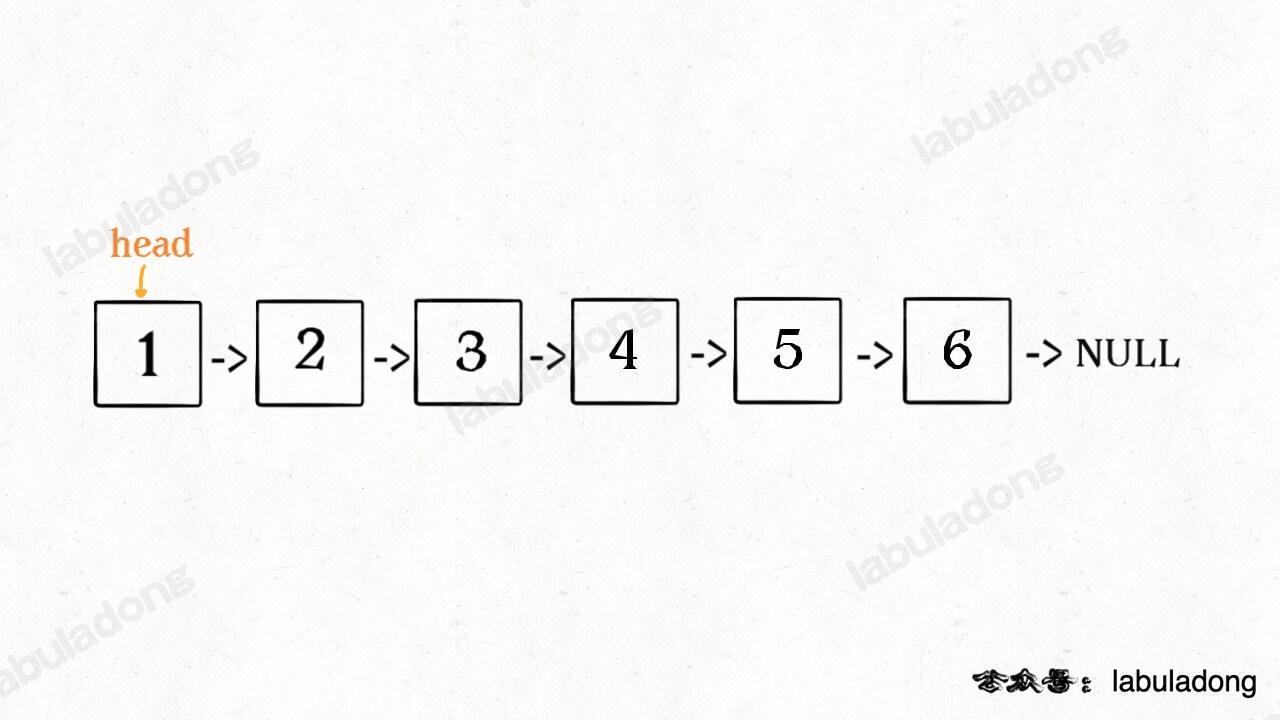
那么输入 reverseList(head) 后,会在这里进行递归:
ListNode last = reverseList(head.next);不要跳进递归(你的脑袋能压几个栈呀?),而是要根据刚才的函数定义,来弄清楚这段代码会产生什么结果:
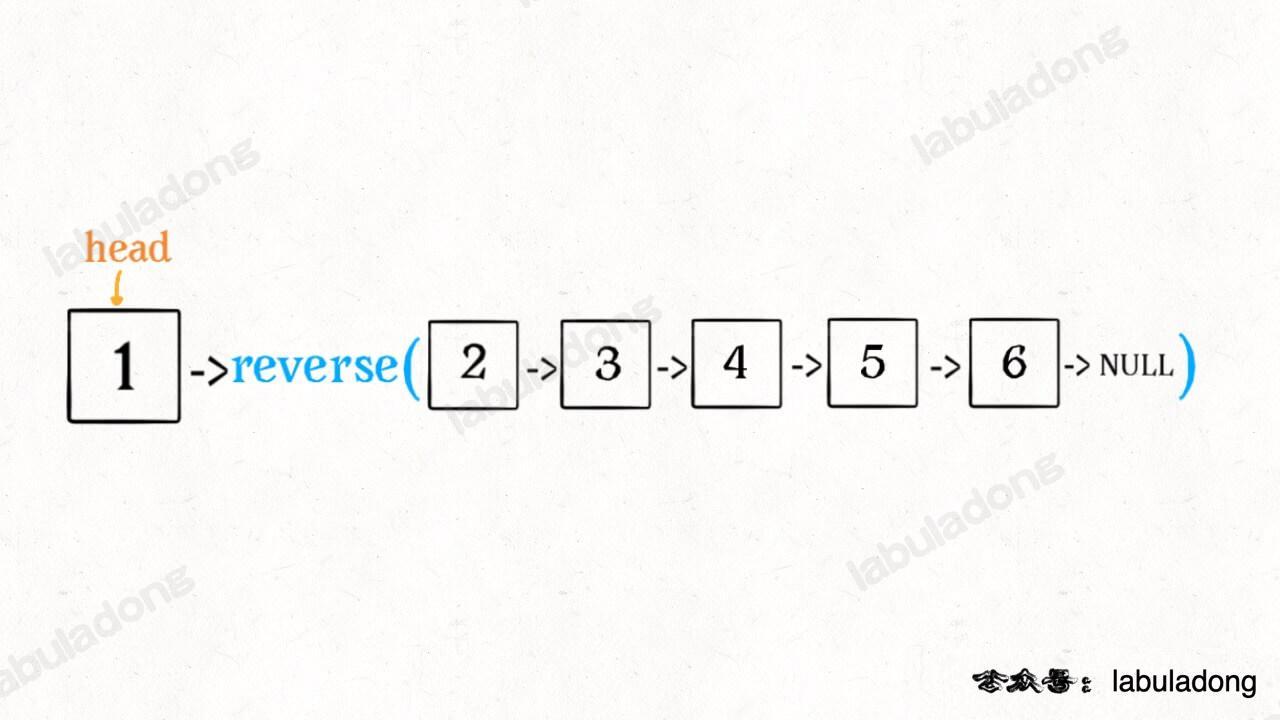
这个 reverseList(head.next) 执行完成后,整个链表就成了这样:
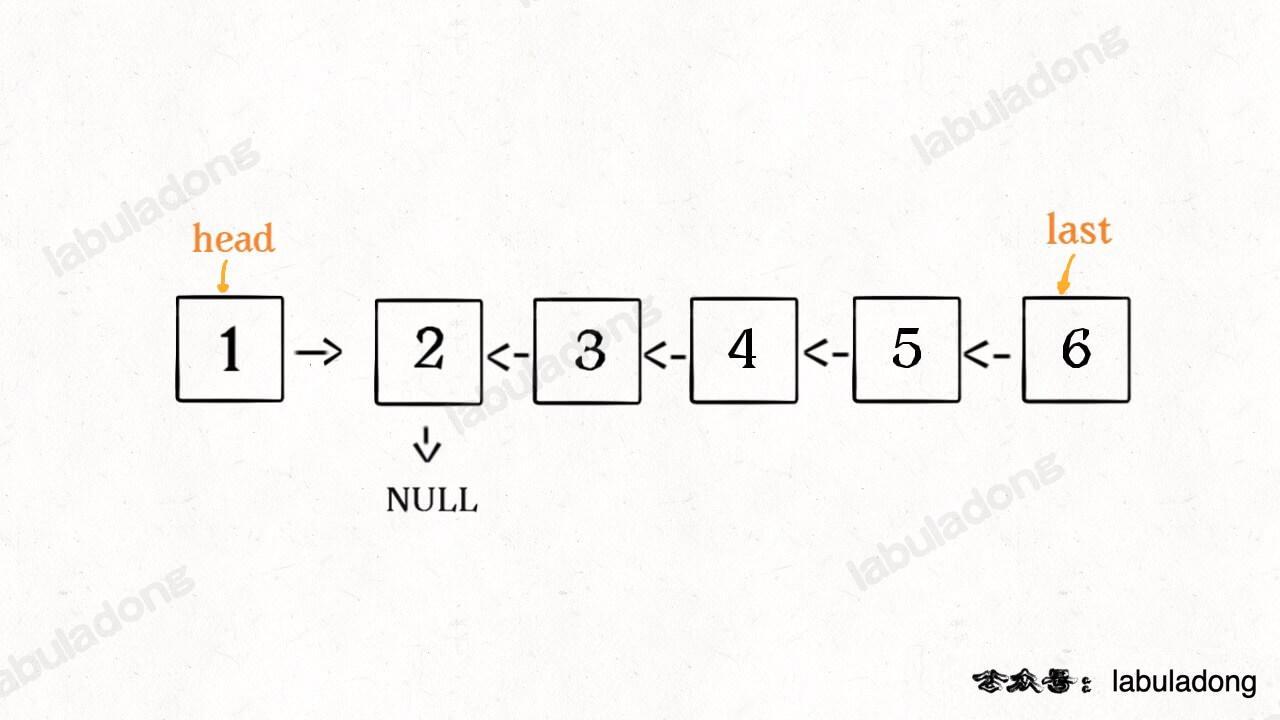
并且根据函数定义,reverseList 函数会返回反转之后的头结点,我们用变量 last 接收了。
现在再来看下面的代码:
head.next.next = head;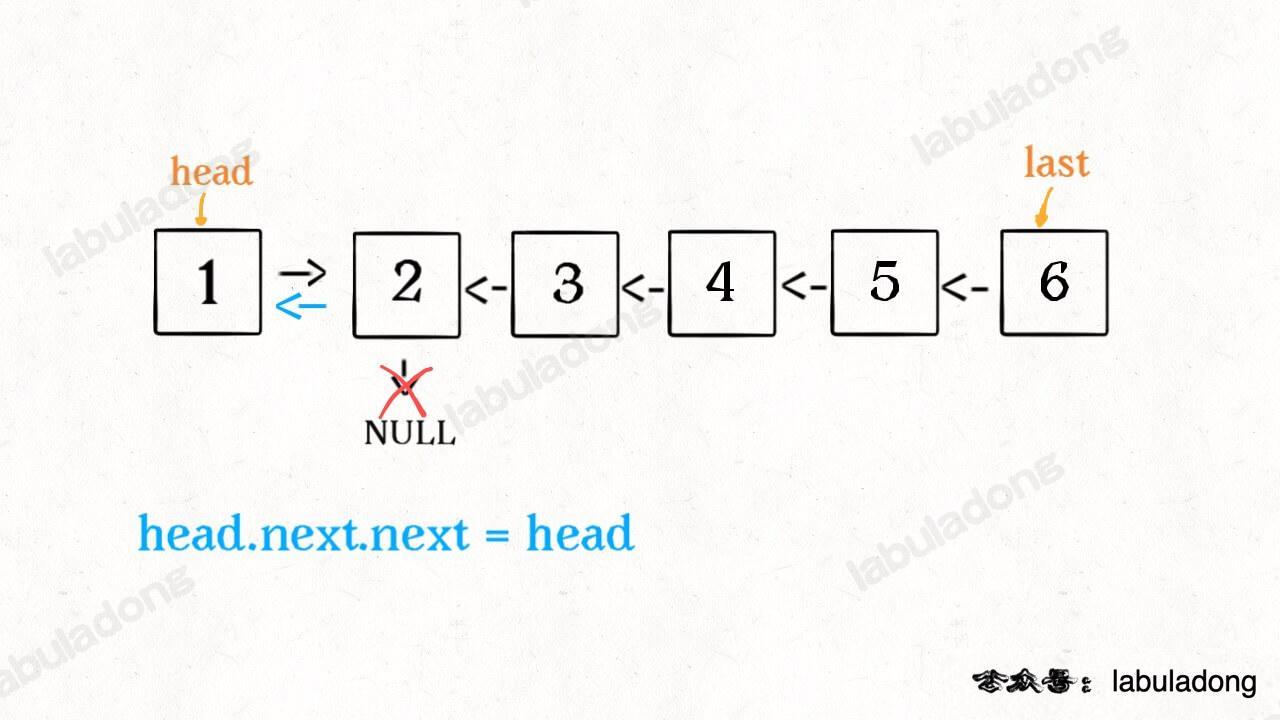
接下来:
head.next = null;
return last;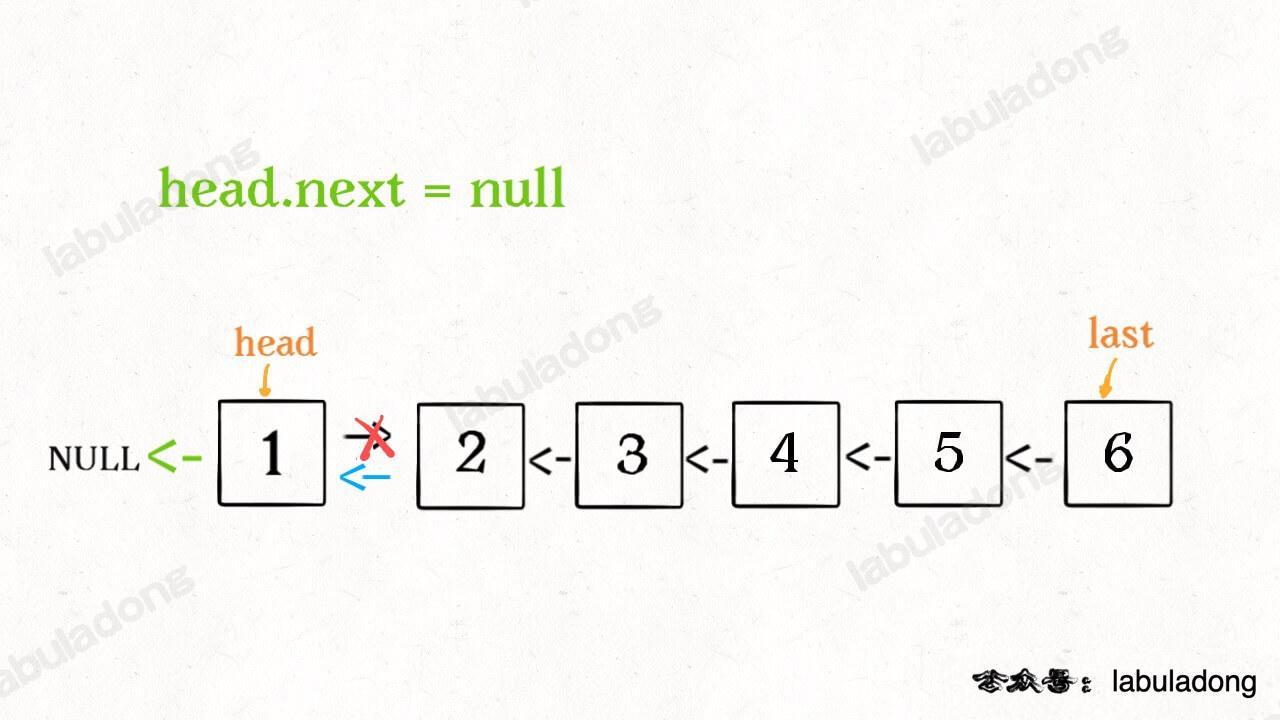
神不神奇,这样整个链表就反转过来了!递归代码就是这么简洁优雅,不过其中有两个地方需要注意:
1、递归函数要有 base case,也就是这句:
if (head == null || head.next == null) {
return head;
}意思是如果链表为空或者只有一个节点的时候,反转结果就是它自己,直接返回即可。
2、当链表递归反转之后,新的头结点是 last,而之前的 head 变成了最后一个节点,别忘了链表的末尾要指向 null:
head.next = null;这样,整个单链表就完成反转了,神不神奇?下面是递归反转链表的可视化过程:
🎃 代码可视化动画🎃
[!NOTE]
虽然可视化面板可以展示整个递归过程的所有细节,但我不建议初学者过于执着于细节。建议先依照上面图示讲解的思维方式理解递归,然后再通过可视化面板加深理解。[!NOTE]
值得一提的是,递归操作链表并不高效。递归解法和迭代解法相比,时间复杂度都是 O(N. ,但是迭代解法的空间复杂度是 O(1),而递归解法需要堆栈,空间复杂度是 O(N)。✅
所以递归操作链表可以用来练习递归思维,但是考虑效率的话还是使用迭代算法更好。
反转链表前 N 个节点
这次我们实现一个这样的函数:
// 将链表的前 n 个节点反转(n <= 链表长度)
ListNode reverseN(ListNode head, int n)比如说对于下图链表,执行 reverseN(head, 3):
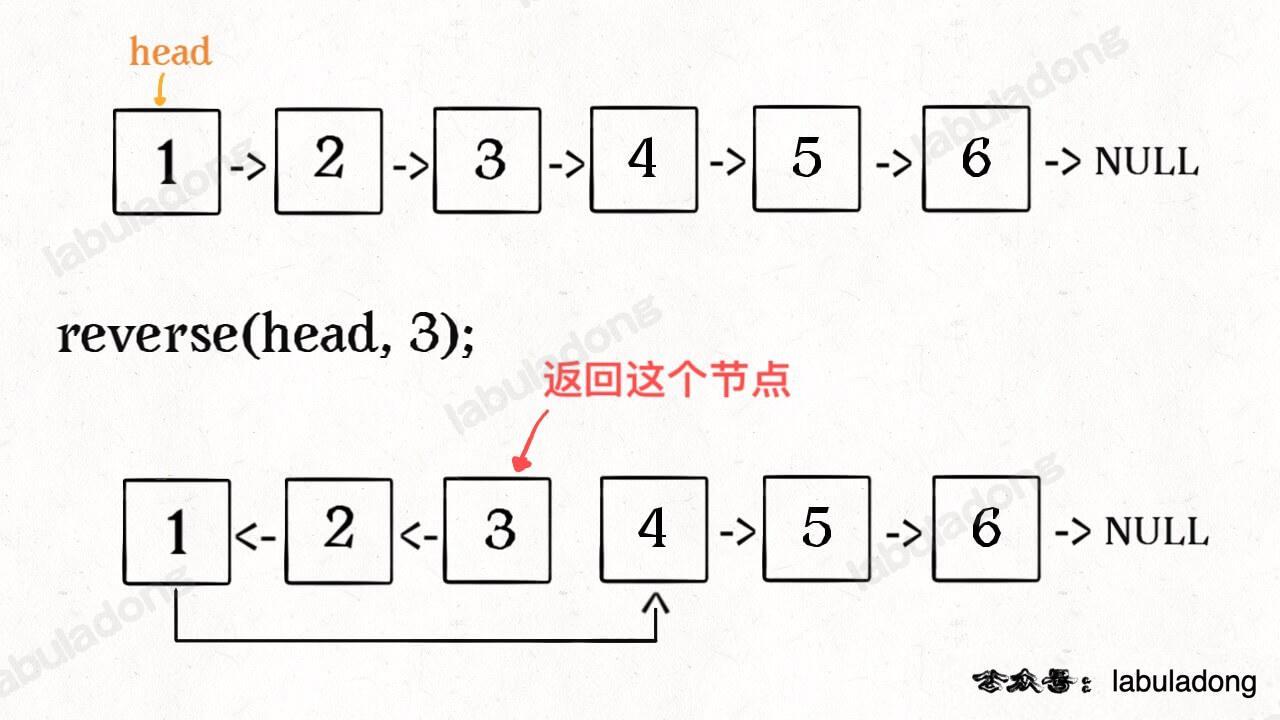
迭代解法
迭代解法应该比较好写,在之前实现的 reverseList 基础上稍加修改就可以了:
ListNode reverseN(ListNode head, int n) {
if (head == null || head.next == null) {
return head;
}
ListNode pre, cur, nxt;
pre = null; cur = head; nxt = head.next;
while (n > 0) {
cur.next = pre;
pre = cur;
cur = nxt;
if (nxt != null) {
nxt = nxt.next;
}
n--;
}
// 此时的 cur 是第 n + 1 个节点,head 是反转后的尾结点
head.next = cur;
// 此时的 pre 是反转后的头结点
return pre;
}
🌟 代码可视化动画🌟
递归解法
递归思路和递归反转整个链表差不多,只要稍加修改即可:
// 后驱节点
ListNode successor = null;
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
// 让反转之后的 head 节点和后面的节点连起来
head.next = successor;
return last;
}具体的区别:
1、base case 变为 n == 1,反转一个元素,就是它本身,同时要记录后驱节点,即要记录第 n + 1 个节点。
2、刚才我们直接把 head.next 设置为 null,因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了,所以要记录后驱 successor(第 n + 1 个节点),反转之后将 head 连接上。

🍭 代码可视化动画🍭
反转链表的一部分
我们可以再进一步,给你一个索引区间,让你把单链表中这部分元素反转,其他部分不变。
力扣第 92 题「反转链表 II」就是这个问题:
题目输入索引区间 [m, n](索引从 1 开始),仅仅反转区间中的链表元素,函数签名如下:
ListNode reverseBetween(ListNode head, int m, int n)迭代解法
纯迭代的思路比较直接,可以先找到第 m - 1 个节点,然后复用之前实现的 reverseN 函数就行了:
class Solution {
public ListNode reverseBetween(ListNode head, int m, int n) {
if (m == 1) {
return reverseN(head, n);
}
// 找到第 m 个节点的前驱
ListNode pre = head;
for (int i = 1; i < m - 1; i++) {
pre = pre.next;
}
// 从第 m 个节点开始反转
pre.next = reverseN(pre.next, n - m + 1);
return head;
}
ListNode reverseN(ListNode head, int n) {
if (head == null || head.next == null) {
return head;
}
ListNode pre, cur, nxt;
pre = null; cur = head; nxt = head.next;
while (n > 0) {
cur.next = pre;
pre = cur;
cur = nxt;
if (nxt != null) {
nxt = nxt.next;
}
n--;
}
// 此时的 cur 是第 n + 1 个节点,head 是反转后的尾结点
head.next = cur;
// 此时的 pre 是反转后的头结点
return pre;
}
}
👾 代码可视化动画👾
递归解法
纯递归解法,依然是找到第 m - 1 个节点,然后复用之前实现的 reverseN 函数就行了。
关键是,如何通过递归的方式找到第 m - 1 个节点呢?
如果我们把 head 的索引视为 1,那么我们是想从第 m 个元素开始反转对吧;如果把 head.next 的索引视为 1 呢?那么相对于 head.next,反转的区间应该是从第 m - 1 个元素开始的;那么对于 head.next.next 呢……
这其实就是用递归的方式来进行迭代。我们可以这样写代码:
class Solution {
public ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
return reverseN(head, n);
}
// 前进到反转的起点触发 base case
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}
// 后驱节点
ListNode successor = null;
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
head.next = successor;
return last;
}
}
🎃 代码可视化动画🎃
K 个一组反转链表
这个问题经常在面经中看到,而且力扣上难度是 Hard,看下题目:
有了前面的层层铺垫,它真的有那么难吗?其实只要你运用一下「分解问题」的思维,然后直接复用前面的 reverseN 函数就行了。
思路分析
认真思考一下可以发现这个问题具有递归性质。
比如说我们对这个链表调用 reverseKGroup(head, 2),即以 2 个节点为一组反转链表:
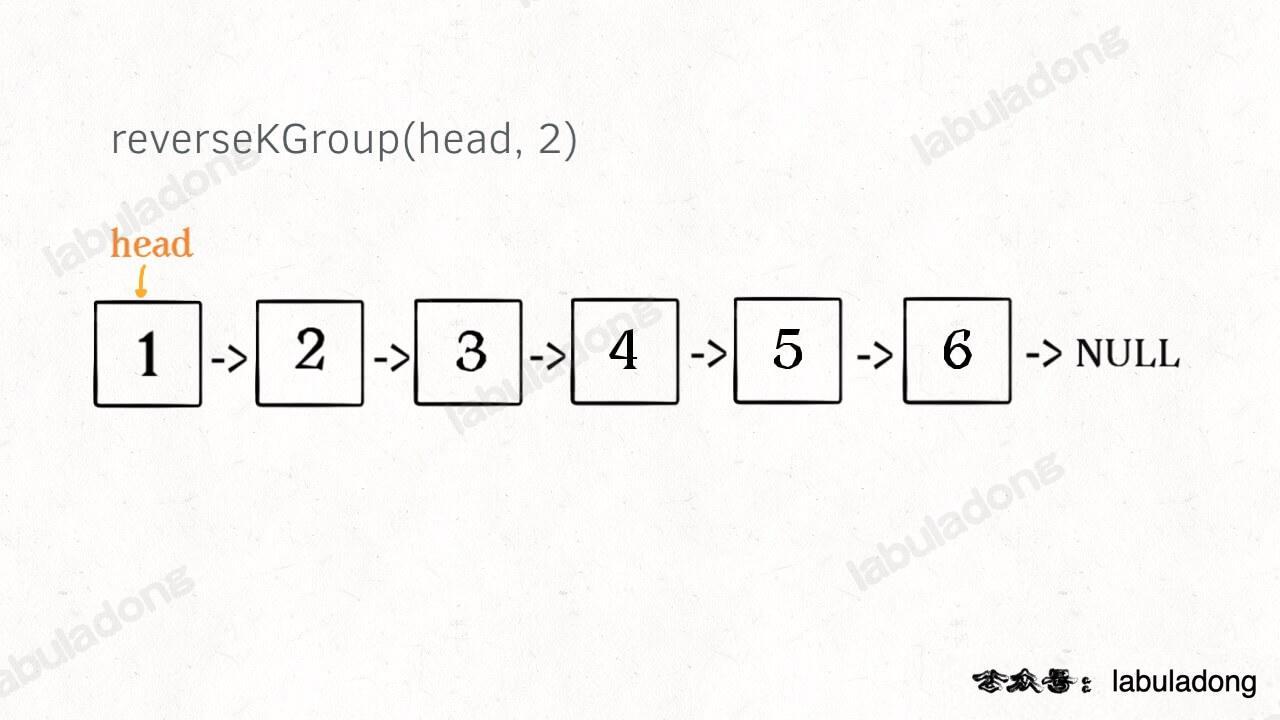
如果我设法把前 2 个节点反转,那么后面的那些节点怎么处理?后面的这些节点也是一条链表,而且规模(长度)比原来这条链表小,这就叫规模更小,结构相同的子问题。
我们可以把原先的 head 指针移动到后面这一段链表的开头,然后继续递归调用 reverseKGroup(head, 2):
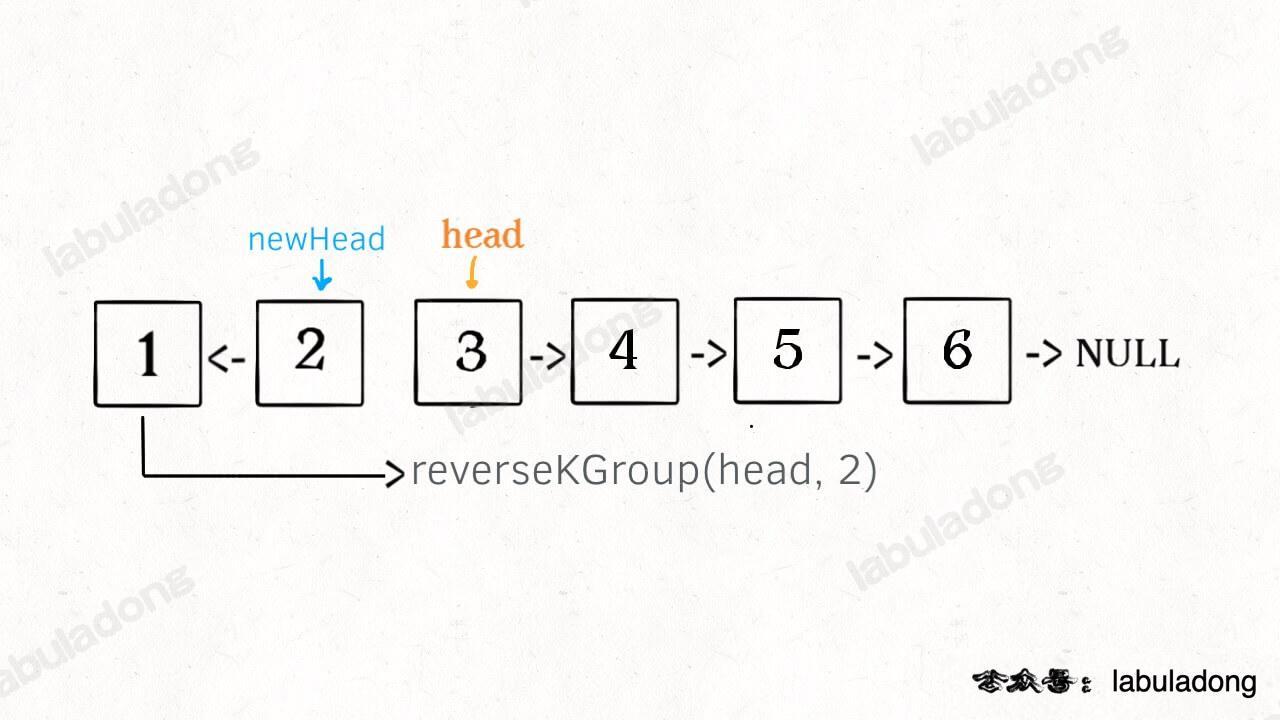
发现了递归性质,就可以得到大致的算法流程:
1、先反转以 head 开头的 k 个元素。这里可以复用前面实现的 reverseN 函数。
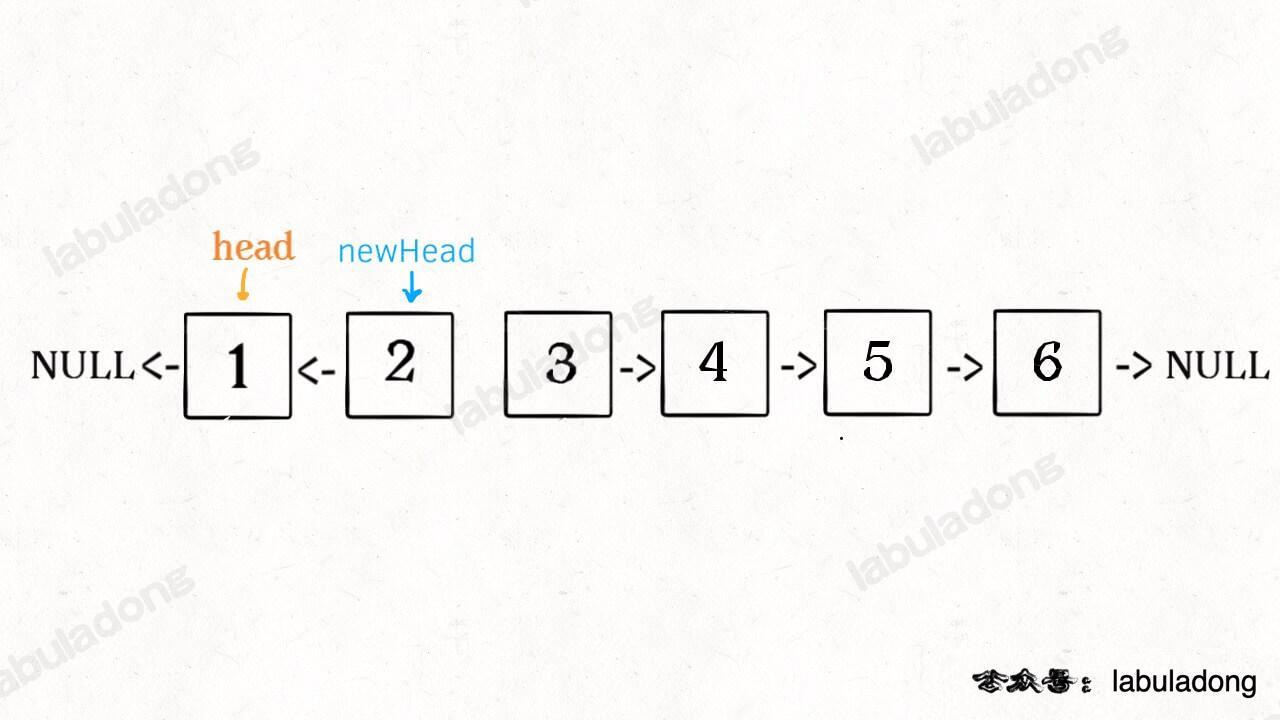
2、将第 k + 1 个元素作为 head 递归调用 reverseKGroup 函数。
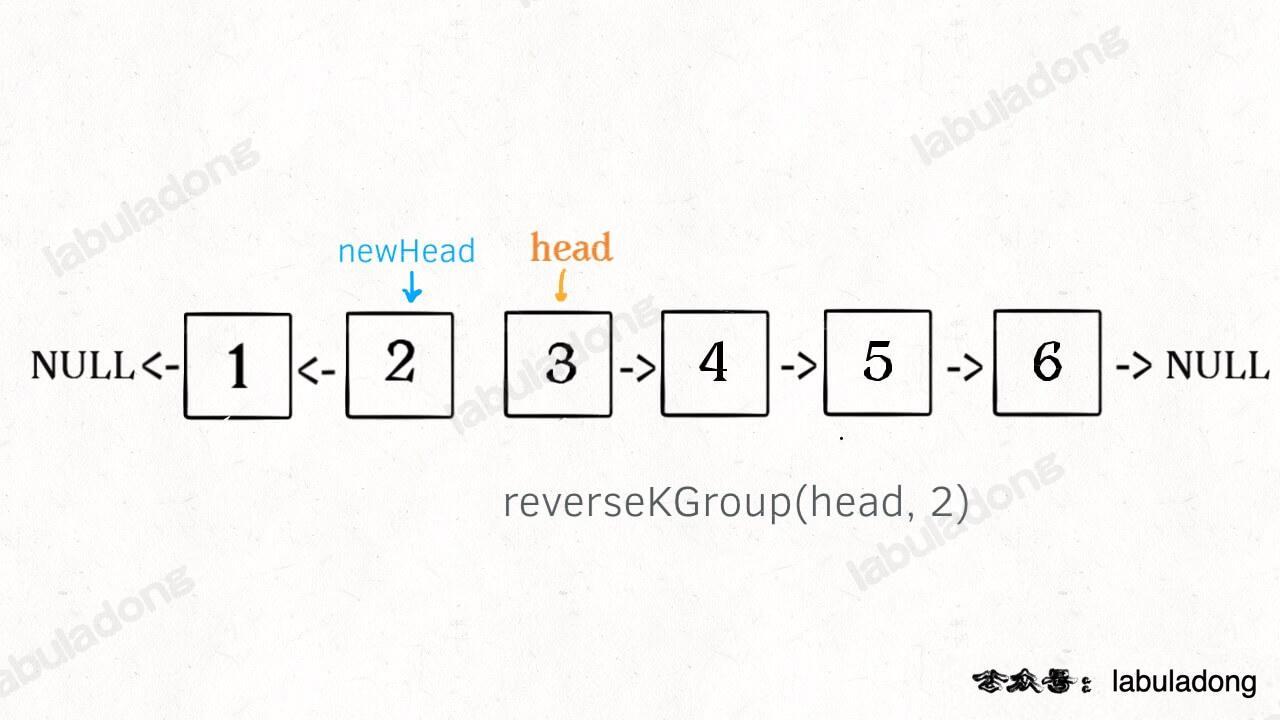
3、将上述两个过程的结果连接起来。
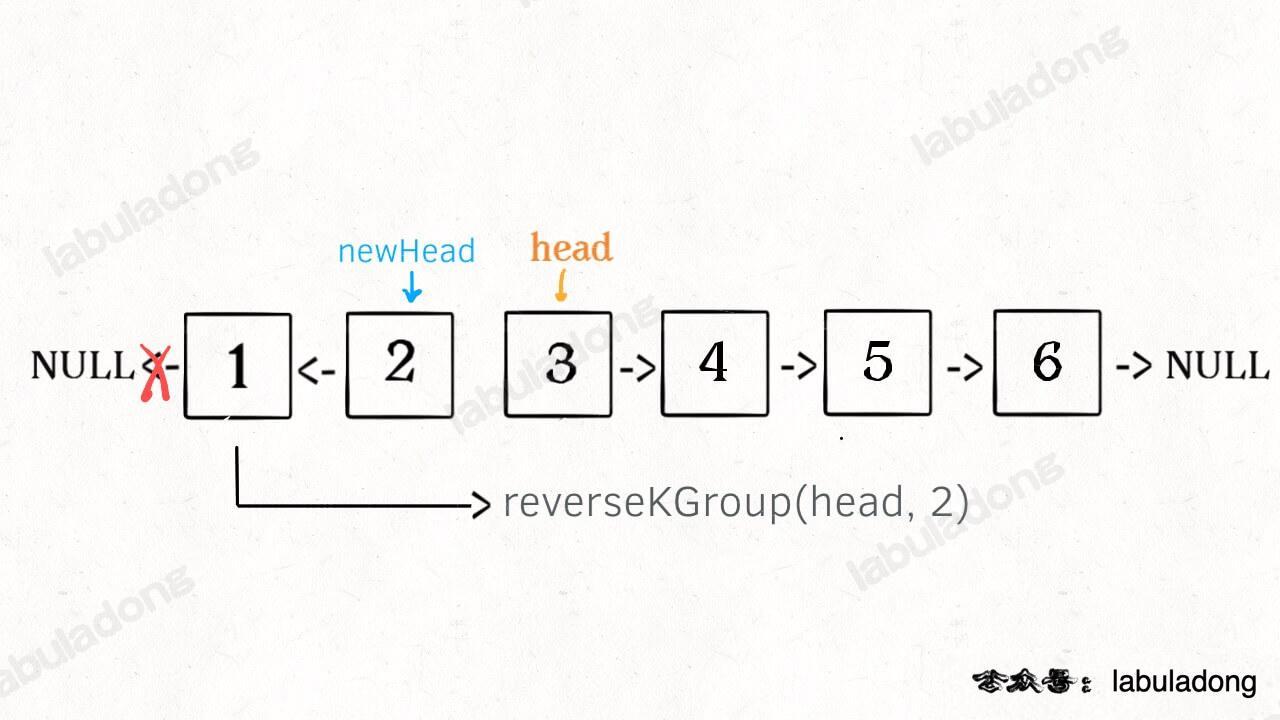
代码实现
结合上面的逐步讲解,代码就可以直接写出来了。我这里就用迭代形式的 reverseN 函数,你想用递归形式的也可以:
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
if (head == null) return null;
// 区间 [a, b) 包含 k 个待反转元素
ListNode a, b;
a = b = head;
for (int i = 0; i < k; i++) {
// 不足 k 个,不需要反转了
if (b == null) return head;
b = b.next;
}
// 反转前 k 个元素
ListNode newHead = reverseN(a, k);
// 此时 b 指向下一组待反转的头结点
// 递归反转后续链表并连接起来
a.next = reverseKGroup(b, k);
return newHead;
}
// 上文实现的反转前 N 个节点的函数
ListNode reverseN(ListNode head, int n) {
if (head == null || head.next == null) {
return head;
}
ListNode pre, cur, nxt;
pre = null; cur = head; nxt = head.next;
while (n > 0) {
cur.next = pre;
pre = cur;
cur = nxt;
if (nxt != null) {
nxt = nxt.next;
}
n--;
}
head.next = cur;
return pre;
}
}很快啊,这道题就解决了。
🌈 代码可视化动画🌈
最后总结
递归的思想相对迭代思想,稍微有点难以理解,处理的技巧是:不要跳进递归,而是利用明确的定义来实现算法逻辑。
处理看起来比较困难的问题,可以尝试化整为零,把一些简单的解法进行修改,解决困难的问题。
引用本文的文章
- [【强化练习】链表双指针经典习题](https://labuladong.online/algo/problem-set/linkedlist-two-pointers/)
- [二叉树心法(思路篇)](https://labuladong.online/algo/data-structure/binary-tree-part1/)
- [如何判断回文链表](https://labuladong.online/algo/data-structure/palindrome-linked-list/)
- [烧饼排序算法](https://labuladong.online/algo/frequency-interview/pancake-sorting/)
- [算法笔试「骗分」套路](https://labuladong.online/algo/other-skills/tips-in-exam/)