环检测及拓扑排序算法

通知:为满足广大读者的需求,网站上架 速成目录,如有需要可以看下,谢谢大家的支持~另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 207. Course Schedule | 207. 课程表 | 🟠 |
| 210. Course Schedule II | 210. 课程表 II | 🟠 |
-----------
[!NOTE]
阅读本文前,你需要先学习:[!IMPORTANT]
进行拓扑排序之前,先要确保图中没有环。图的「逆后序遍历」顺序,就是拓扑排序的结果。
图这种数据结构有一些比较特殊的算法,比如二分图判断,有环图无环图的判断,拓扑排序,以及最经典的最小生成树,单源最短路径问题,更难的就是类似网络流这样的问题。
不过目前来看,像网络流这种问题,你又不是打竞赛的,没时间的话就没必要学了;像 最小生成树 和 最短路径问题,虽然从刷题的角度遇到的不多,但它们属于经典算法,学有余力可以掌握一下;像 二分图判定、拓扑排序这一类,本质上就是图的遍历,属于比较基本的算法,应该熟练地掌握。
那么本文就结合具体的算法题,来说两个图论算法:有向图的环检测、拓扑排序算法。
这两个算法既可以用 DFS 思路解决,也可以用 BFS 思路解决,相对而言 BFS 解法从代码实现上看更简洁一些,但 DFS 解法有助于你进一步理解递归遍历数据结构的奥义,所以本文中我先讲 DFS 遍历的思路,再讲 BFS 遍历的思路。
环检测算法(DFS 版本)
先来看看力扣第 207 题「课程表」:
// 函数签名如下
boolean canFinish(int numCourses, int[][] prerequisites);题目应该不难理解,什么时候无法修完所有课程?当存在循环依赖的时候。
其实这种场景在现实生活中也十分常见,比如我们写代码 import 包也是一个例子,必须合理设计代码目录结构,否则会出现循环依赖,编译器会报错,所以编译器实际上也使用了类似算法来判断你的代码是否能够成功编译。
看到依赖问题,首先想到的就是把问题转化成「有向图」这种数据结构,只要图中存在环,那就说明存在循环依赖。
具体来说,我们首先可以把课程看成「有向图」中的节点,节点编号分别是 0, 1, ..., numCourses-1,把课程之间的依赖关系看做节点之间的有向边。
比如说必须修完课程 1 才能去修课程 3,那么就有一条有向边从节点 1 指向 3。
所以我们可以根据题目输入的 prerequisites 数组生成一幅类似这样的图:
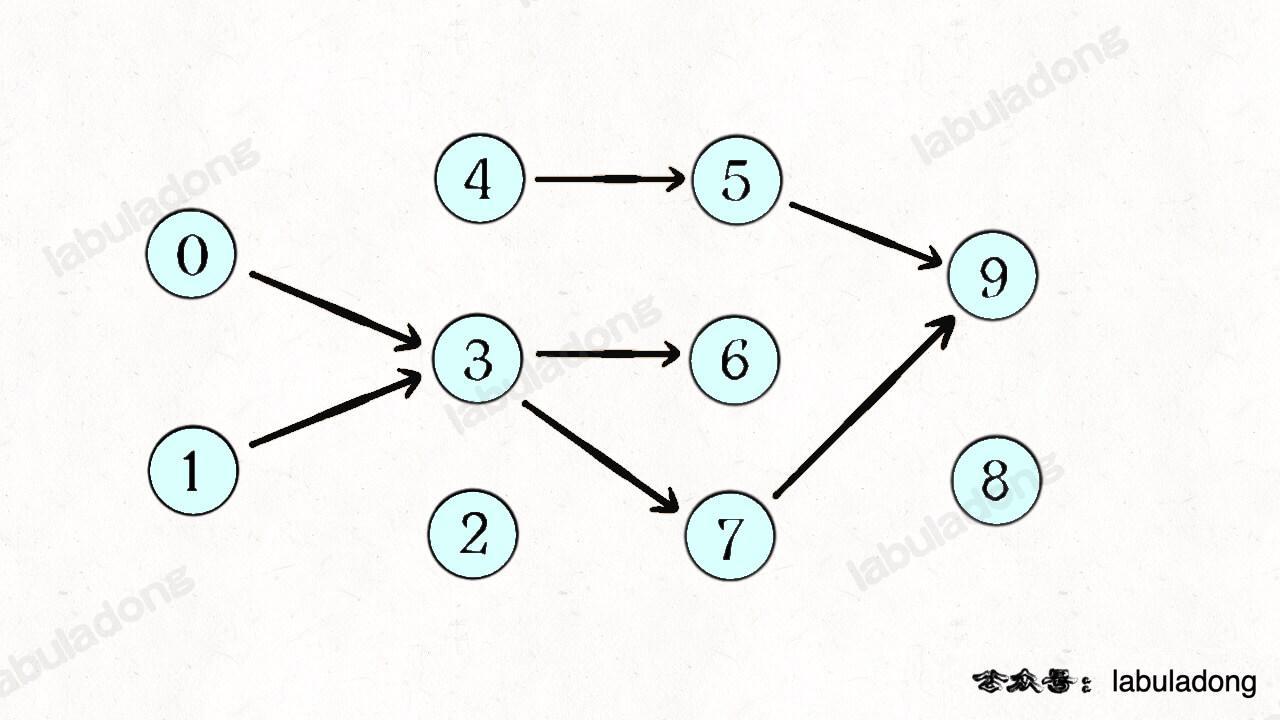
如果发现这幅有向图中存在环,那就说明课程之间存在循环依赖,肯定没办法全部上完;反之,如果没有环,那么肯定能上完全部课程。
好,那么想解决这个问题,首先我们要把题目的输入转化成一幅有向图,然后再判断图中是否存在环。
如何转换成图呢?我们前文 图结构的存储 写过图的两种存储形式,邻接矩阵和邻接表。
这里我就用邻接表形式存储图吧,首先可以写一个建图函数:
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 图中共有 numCourses 个节点
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
// 添加一条从 from 指向 to 的有向边
// 边的方向是「被依赖」关系,即修完课程 from 才能修课程 to
graph[from].add(to);
}
return graph;
}图建出来了,怎么判断图中有没有环呢?
很简单,无非就是想考你如何遍历图中的所有路径嘛,如果我能遍历所有路径,那么路径是否成环不就容易算出来了吗?
图的 DFS/BFS 遍历基础 写了如何用 DFS 算法遍历图的所有路径,如果忘记了请去复习,下面要用到。
我这里先直接套用遍历所有路径的 DFS 代码模板,用一个 hasCycle 变量记录是否存在环,当重复遍历到 onPath 中的节点时,就说明遇到了环,设置 hasCycle = true。
基于这个思路,先看第一版代码(会超时):
class Solution {
// 记录递归堆栈中的节点
boolean[] onPath;
// 记录图中是否有环
boolean hasCycle = false;
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
onPath = new boolean[numCourses];
for (int i = 0; i < numCourses; i++) {
// 遍历图中的所有节点
traverse(graph, i);
}
// 只要没有循环依赖可以完成所有课程
return !hasCycle;
}
// 图遍历函数,遍历所有路径
void traverse(List<Integer>[] graph, int s) {
if (hasCycle) {
// 如果已经找到了环,也不用再遍历了
return;
}
if (onPath[s]) {
// s 已经在递归路径上,说明成环了
hasCycle = true;
return;
}
// 前序代码位置
onPath[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 后序代码位置
onPath[s] = false;
}
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 代码见前文
}
}注意图中并不是所有节点都相连,所以要用一个 for 循环将所有节点都作为起点调用一次 DFS 搜索算法。
其实这个解法已经是正确的了,因为遍历了所有路径,一定可以判定是否成环。但是这个解法无法通过所有测试用例,会超时。那么原因肯定也能猜出来,有冗余计算呗。
哪里有冗余计算呢?我举个例子你就明白了。
假设现在你以节点 2 为起点遍历所有可达的路径,最终发现没有环。
假设另一个节点 5 有一条指向 2 的边,你在以 5 为起点遍历所有可达的路径时,肯定还会走到 2,那么请问,此时你是否还需要继续遍历 2 的所有可达路径呢?
答案是不需要了,因为第一次你没找到环,那么这次也不可能找到环。想明白这里面的冗余计算没有?你如果觉得有反例,可以自己画一下,实际上是没有反例的。
那么对症下药就行了:如果我们发现一个节点之前被遍历过,就可以直接跳过,不用再重复遍历了。
优化后的代码如下:
class Solution {
// 记录一次递归堆栈中的节点
boolean[] onPath;
// 记录节点是否被遍历过
boolean[] visited;
// 记录图中是否有环
boolean hasCycle = false;
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
onPath = new boolean[numCourses];
visited = new boolean[numCourses];
for (int i = 0; i < numCourses; i++) {
// 遍历图中的所有节点
traverse(graph, i);
}
// 只要没有循环依赖可以完成所有课程
return !hasCycle;
}
// 图遍历函数,遍历所有路径
void traverse(List<Integer>[] graph, int s) {
if (hasCycle) {
// 如果已经找到了环,也不用再遍历了
return;
}
if (onPath[s]) {
// s 已经在递归路径上,说明成环了
hasCycle = true;
return;
}
if (visited[s]) {
// 不用再重复遍历已遍历过的节点
return;
}
// 前序代码位置
visited[s] = true;
onPath[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 后序代码位置
onPath[s] = false;
}
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 代码见前文
}
}`visited` 为 true 的节点为绿色,`onPath` 为 true 的节点为橙色。
你可以打开可视化面板,多次点击 if (onPath[s]) 这部分代码,即可查看 DFS 遍历图的过程。
这道题就解决了,核心就是判断一幅有向图中是否存在环。
不过如果出题人继续提问,让你不仅要判断是否存在环,还要返回这个环具体有哪些节点,怎么办?
你可能说,onPath 里面为 true 的索引,不就是组成环的节点编号吗?
不是的,假设从节点 0 开始遍历,下图中绿色的节点是递归的路径,它们在 onPath 中的值都是 true,但显然成环的节点只是其中的一部分:
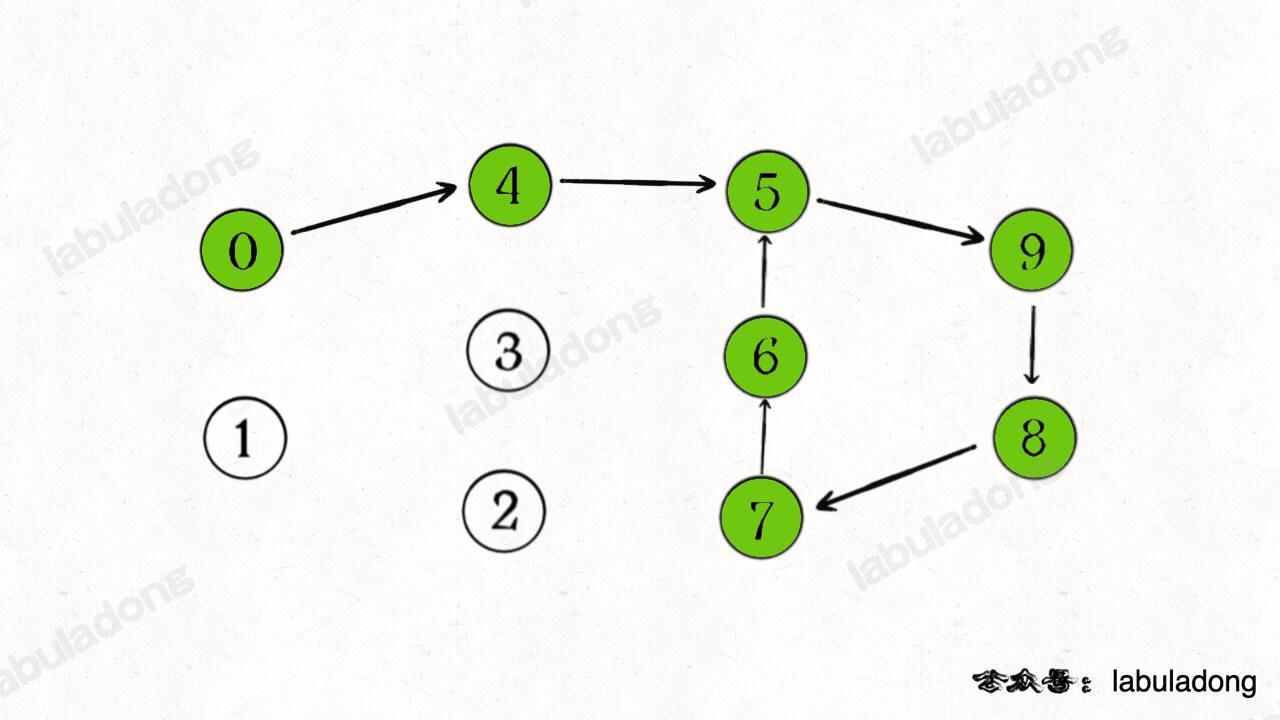
这个问题大家可以先思考一下,办法肯定有很多啦,我只给出一个常用的解法。
[!NOTE]
最简单直接的解法是,在boolean[] onPath数组的基础上,我们再使用一个Stack<Integer> path栈,把遍历过程中经过的节点顺序也保存下来。比如按照上图绿色的遍历顺序,
path从栈底到栈顶的元素就是[0,4,5,9,8,7,6]。此时又一次遇到了节点5,那么就可以知道[5,9,8,7,6]这部分是环了。
接下来,我们来再讲一个经典的图算法:拓扑排序。
拓扑排序算法(DFS 版本)
看下力扣第 210 题「课程表 II」:
这道题就是上道题的进阶版,不是仅仅让你判断是否可以完成所有课程,而是进一步让你返回一个合理的上课顺序,保证开始修每个课程时,前置的课程都已经修完。
函数签名如下:
int[] findOrder(int numCourses, int[][] prerequisites);这里我先说一下拓扑排序(Topological Sorting)这个名词,网上搜出来的定义很数学,这里干脆用百度百科的一幅图来让你直观地感受下:
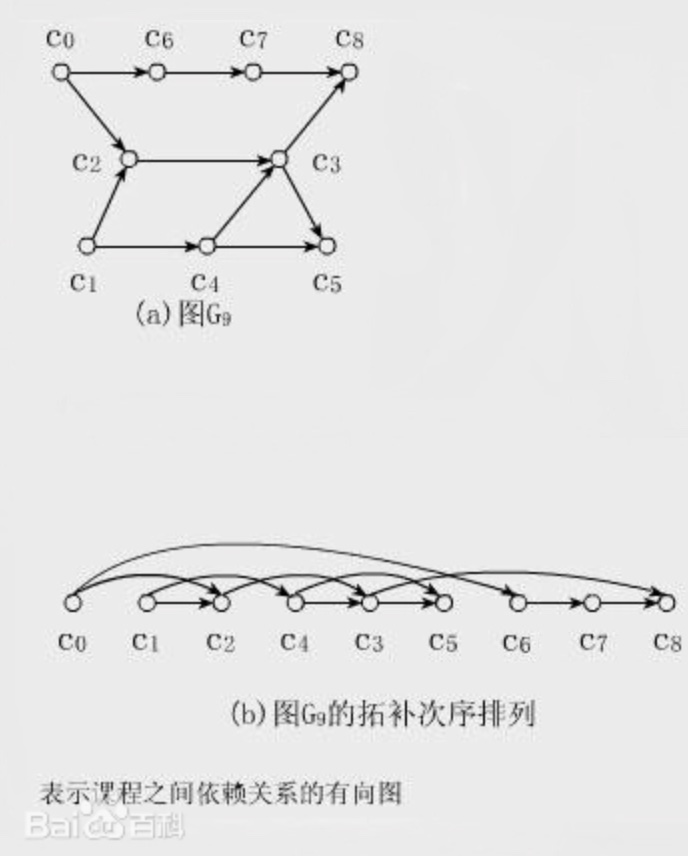
直观地说就是,让你把一幅图「拉平」,而且这个「拉平」的图里面,所有箭头方向都是一致的,比如上图所有箭头都是朝右的。
很显然,如果一幅有向图中存在环,是无法进行拓扑排序的,因为肯定做不到所有箭头方向一致;反过来,如果一幅图是「有向无环图」,那么一定可以进行拓扑排序。
但是我们这道题和拓扑排序有什么关系呢?
其实也不难看出来,如果把课程抽象成节点,课程之间的依赖关系抽象成有向边,那么这幅图的拓扑排序结果就是上课顺序。
首先,我们先判断一下题目输入的课程依赖是否成环,成环的话是无法进行拓扑排序的,所以我们可以复用上一道题的主函数:
public int[] findOrder(int numCourses, int[][] prerequisites) {
if (!canFinish(numCourses, prerequisites)) {
// 不可能完成所有课程
return new int[]{};
}
// ...
}那么关键问题来了,如何进行拓扑排序?是不是又要秀什么高大上的技巧了?
其实特别简单,把图结构后序遍历的结果进行反转,就是拓扑排序的结果。
::: note 需要反转吗?
有的读者提到,他在网上看到的拓扑排序算法就是后序遍历结果,不用对后序遍历结果进行反转,这是为什么呢?
你确实可以看到这样的解法,原因是他建图的时候对边的定义和我不同。我建的图中箭头方向是「被依赖」关系,比如节点 1 指向 2,含义是节点 1 被节点 2 依赖,即做完 1 才能去做 2,因为这样更符合我们的直觉。
如果你反过来,把有向边定义为「依赖」关系,那么整幅图中边全部反转,就可以不对后序遍历结果反转。具体来说,就是把我的解法代码中 graph[from].add(to); 改成 graph[to].add(from); 就可以不反转了。
:::
直接看解法代码吧,在上一题环检测的代码基础上添加了记录后序遍历结果的逻辑:
class Solution {
// 记录后序遍历结果
List<Integer> postorder = new ArrayList<>();
// 记录是否存在环
boolean hasCycle = false;
boolean[] visited, onPath;
// 主函数
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
// 遍历图
for (int i = 0; i < numCourses; i++) {
traverse(graph, i);
}
// 有环图无法进行拓扑排序
if (hasCycle) {
return new int[]{};
}
// 逆后序遍历结果即为拓扑排序结果
Collections.reverse(postorder);
int[] res = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
res[i] = postorder.get(i);
}
return res;
}
// 图遍历函数
void traverse(List<Integer>[] graph, int s) {
if (onPath[s]) {
// 发现环
hasCycle = true;
}
if (visited[s] || hasCycle) {
return;
}
// 前序遍历位置
onPath[s] = true;
visited[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 后序遍历位置
postorder.add(s);
onPath[s] = false;
}
// 建图函数
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 代码见前文
}
}`visited` 为 true 的节点为绿色,`onPath` 为 true 的节点为橙色。
你可以打开可视化面板,多次点击 if (onPath[s]) 这部分代码,即可查看 DFS 遍历图的过程。
代码虽然看起来多,但是逻辑应该是很清楚的,只要图中无环,那么我们就调用 traverse 函数对图进行 DFS 遍历,记录后序遍历结果,最后把后序遍历结果反转,作为最终的答案。
那么为什么后序遍历的反转结果就是拓扑排序呢?
我这里也避免数学证明,用一个直观地例子来解释,我们就说二叉树,这是我们说过很多次的二叉树遍历框架:
void traverse(TreeNode root) {
// 前序遍历代码位置
traverse(root.left)
// 中序遍历代码位置
traverse(root.right)
// 后序遍历代码位置
}二叉树的后序遍历是什么时候?遍历完左右子树之后才会执行后序遍历位置的代码。换句话说,当左右子树的节点都被装到结果列表里面了,根节点才会被装进去。
后序遍历的这一特点很重要,之所以拓扑排序的基础是后序遍历,是因为一个任务必须等到它依赖的所有任务都完成之后才能开始开始执行。
你把二叉树理解成一幅有向图,边的方向是由父节点指向子节点,那么就是下图这样:
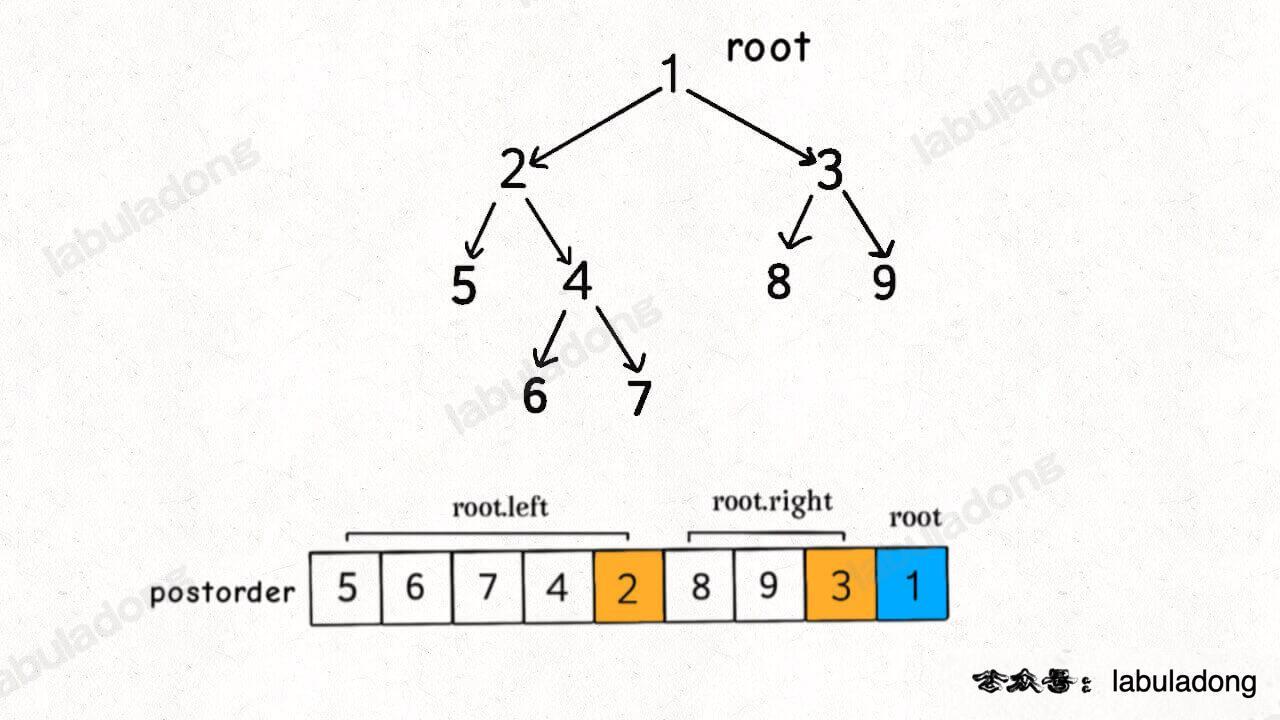
对于标准的后序遍历结果,根节点出现在最后,只要把遍历结果反过来,就是拓扑排序结果:
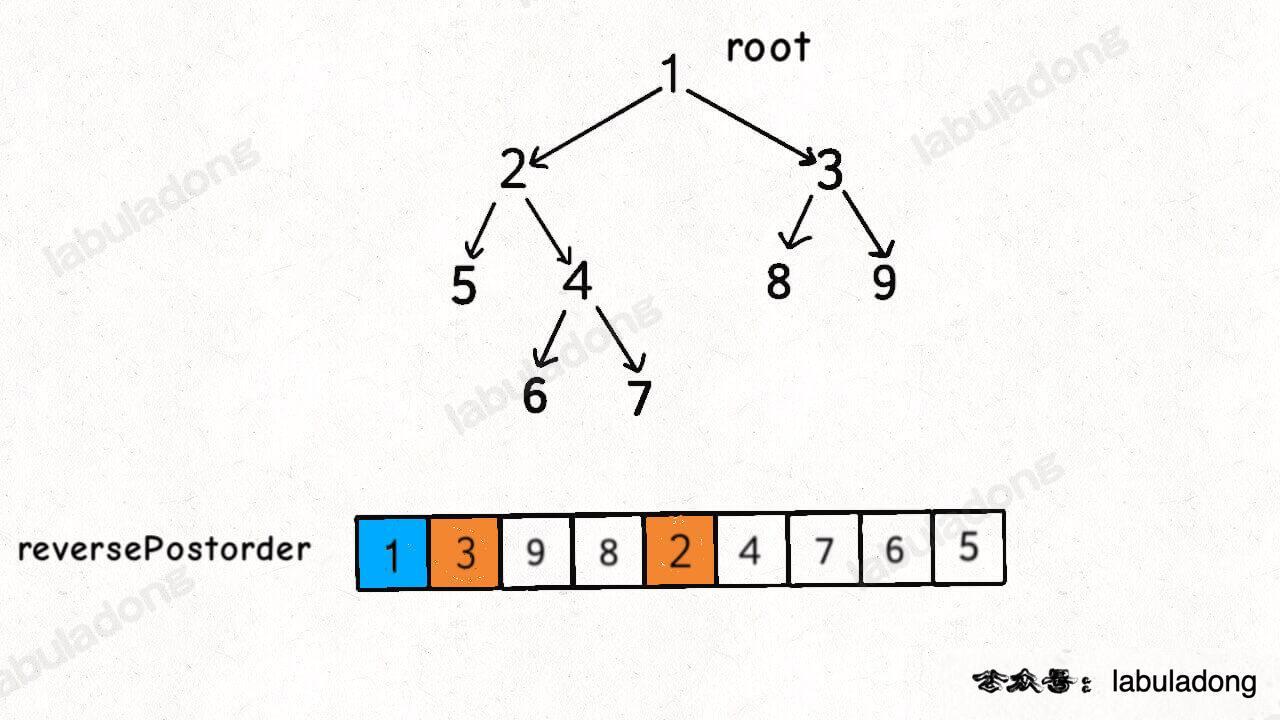
我知道有读者会问,后序遍历结果反转,和前序遍历结果有什么关系?
对于二叉树来说你看起来好像有关系,实际上二者没有任何关系。你千万不要认为后序遍历反转的结果等同于前序遍历结果。
它俩的关键区别在 二叉树思想(纲领篇) 已经讲过了,后序位置的代码是等到左右子树都遍历完才执行的,只有它才能体现出「依赖」关系,其他遍历顺序都做不到。
环检测算法(BFS 版本)
刚才讲了用 DFS 算法利用 onPath 数组判断是否存在环;也讲了用 DFS 算法利用逆后序遍历进行拓扑排序。
其实 BFS 算法借助 indegree 数组记录每个节点的「入度」,也可以实现这两个算法。不熟悉 BFS 算法的读者可阅读前文 BFS 算法核心框架。
所谓「出度」和「入度」是「有向图」中的概念,很直观:如果一个节点 x 有 a 条边指向别的节点,同时被 b 条边所指,则称节点 x 的出度为 a,入度为 b。
先说环检测算法,直接看 BFS 的解法代码:
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
// 建图,有向边代表「被依赖」关系
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
// 构建入度数组
int[] indegree = new int[numCourses];
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
// 节点 to 的入度加一
indegree[to]++;
}
// 根据入度初始化队列中的节点
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0) {
// 节点 i 没有入度,即没有依赖的节点
// 可以作为拓扑排序的起点,加入队列
q.offer(i);
}
}
// 记录遍历的节点个数
int count = 0;
// 开始执行 BFS 循环
while (!q.isEmpty()) {
// 弹出节点 cur,并将它指向的节点的入度减一
int cur = q.poll();
count++;
for (int next : graph[cur]) {
indegree[next]--;
if (indegree[next] == 0) {
// 如果入度变为 0,说明 next 依赖的节点都已被遍历
q.offer(next);
}
}
}
// 如果所有节点都被遍历过,说明不成环
return count == numCourses;
}
// 建图函数
List<Integer>[] buildGraph(int n, int[][] edges) {
// 见前文
}
}我先总结下这段 BFS 算法的思路:
1、构建邻接表,和之前一样,边的方向表示「被依赖」关系。
2、构建一个 indegree 数组记录每个节点的入度,即 indegree[i] 记录节点 i 的入度。
3、对 BFS 队列进行初始化,将入度为 0 的节点首先装入队列。
4、开始执行 BFS 循环,不断弹出队列中的节点,减少相邻节点的入度,并将入度变为 0 的节点加入队列。
5、如果最终所有节点都被遍历过(count 等于节点数),则说明不存在环,反之则说明存在环。
我画个图你就容易理解了,比如下面这幅图,节点中的数字代表该节点的入度:
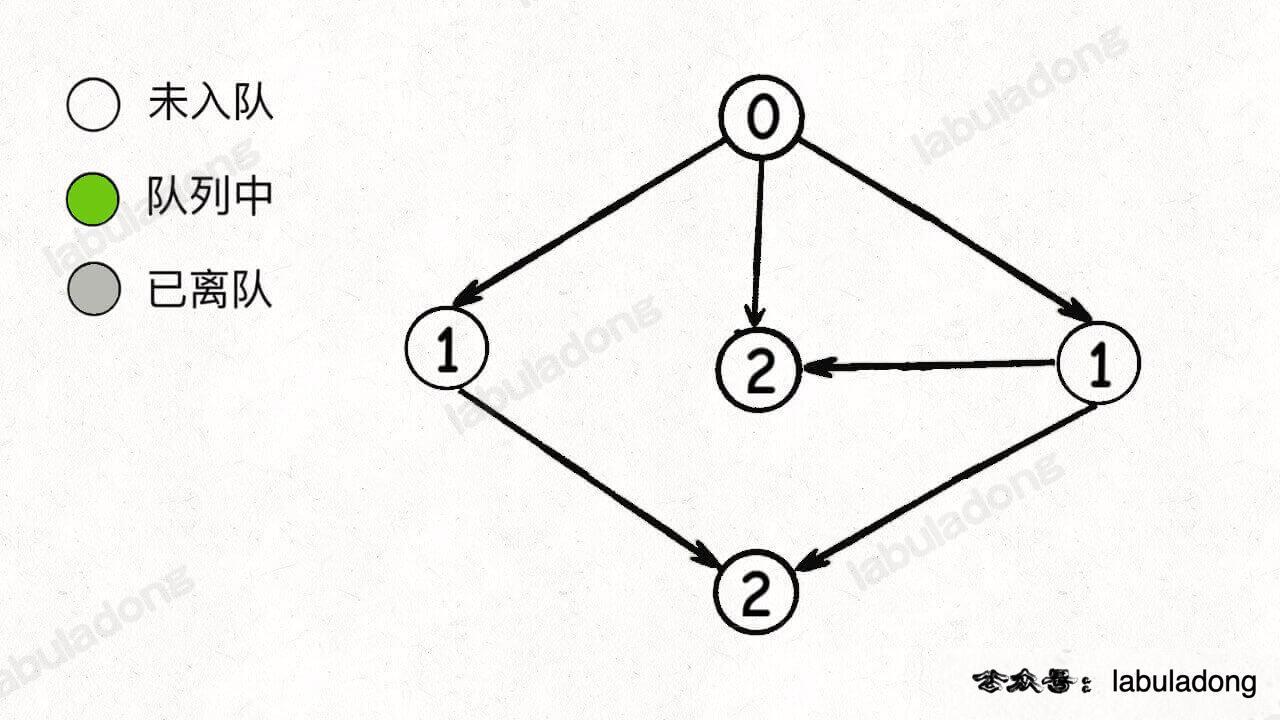
队列进行初始化后,入度为 0 的节点首先被加入队列:
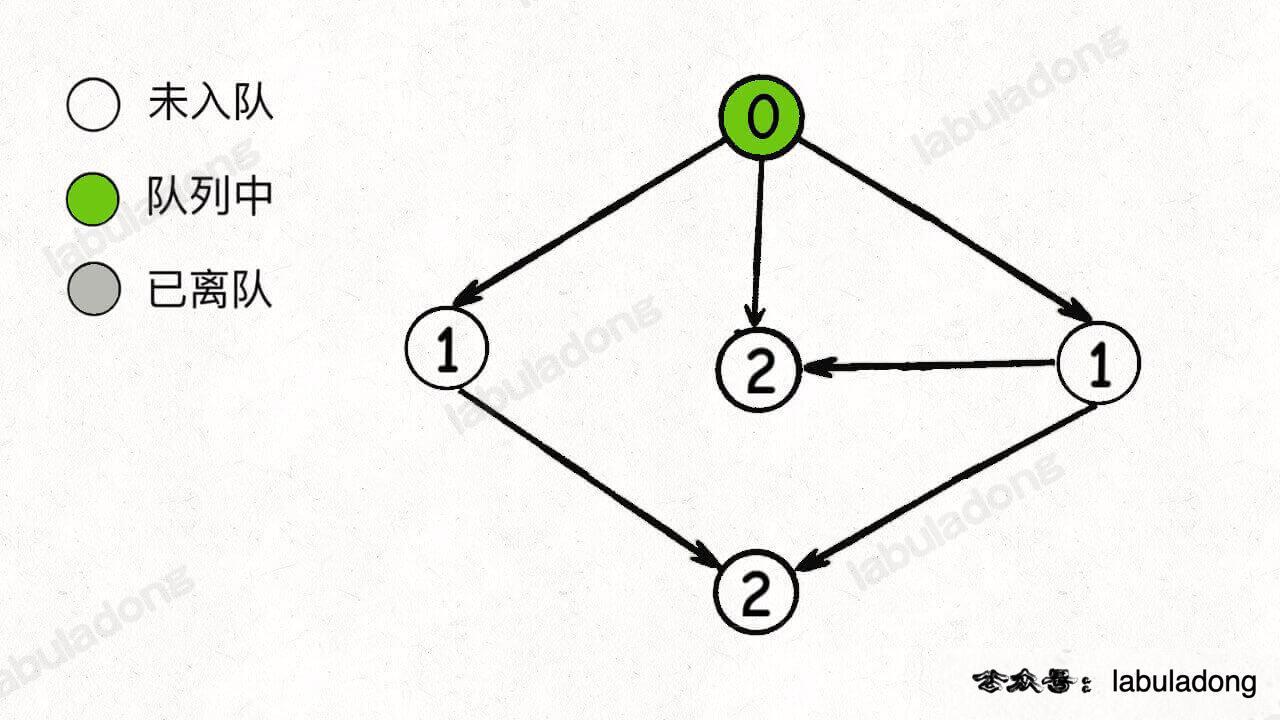
开始执行 BFS 循环,从队列中弹出一个节点,减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
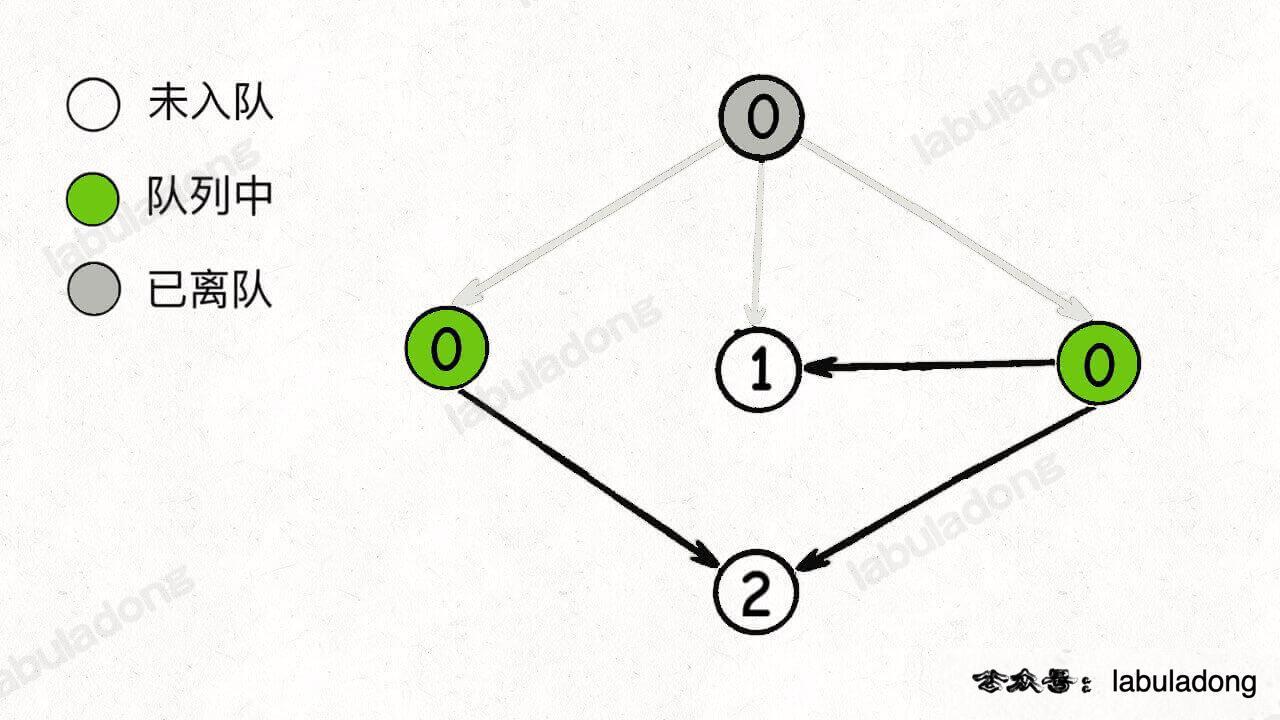
继续从队列弹出节点,并减少相邻节点的入度,这一次没有新产生的入度为 0 的节点:
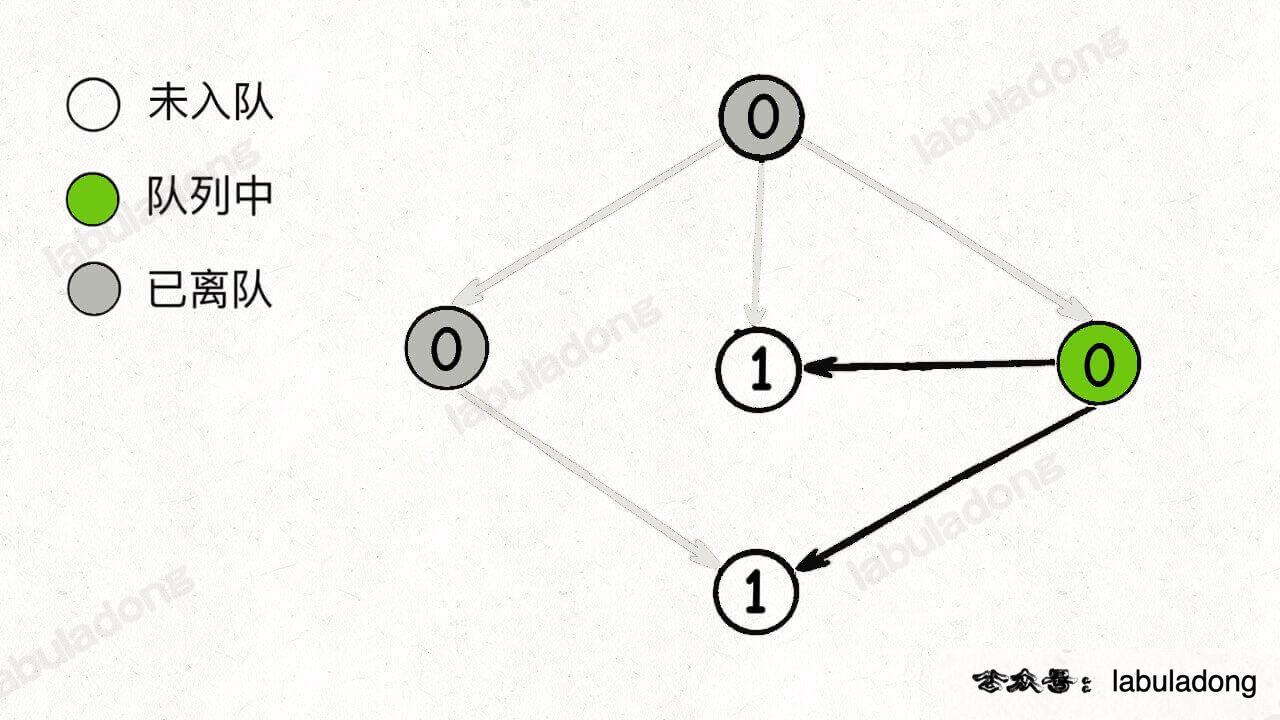
继续从队列弹出节点,并减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
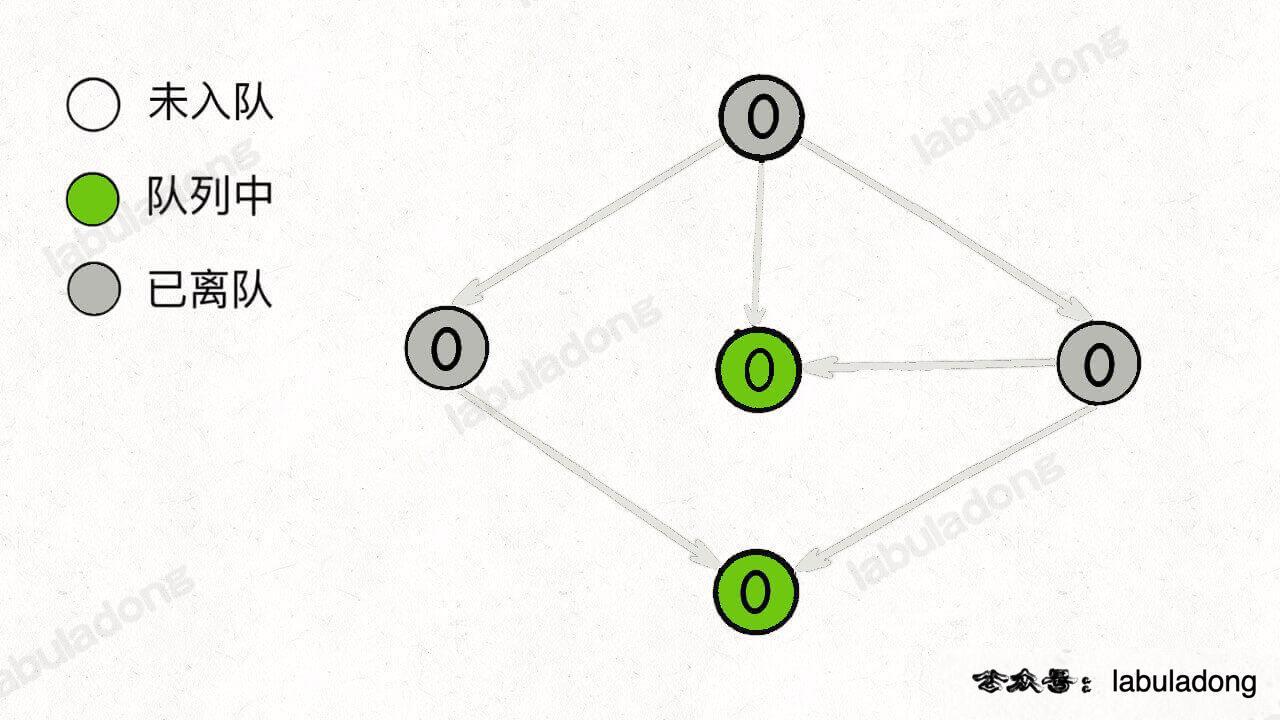
继续弹出节点,直到队列为空:
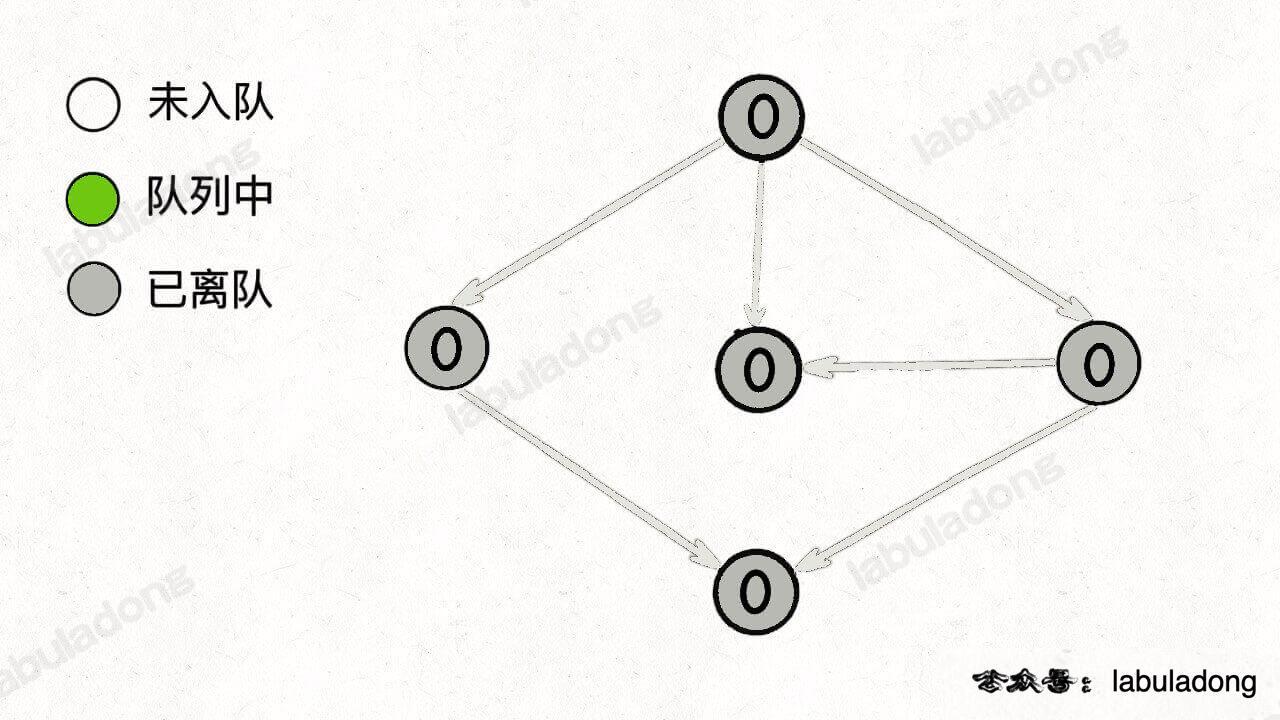
这时候,所有节点都被遍历过一遍,也就说明图中不存在环。
反过来说,如果按照上述逻辑执行 BFS 算法,存在节点没有被遍历,则说明成环。
比如下面这种情况,队列中最初只有一个入度为 0 的节点:
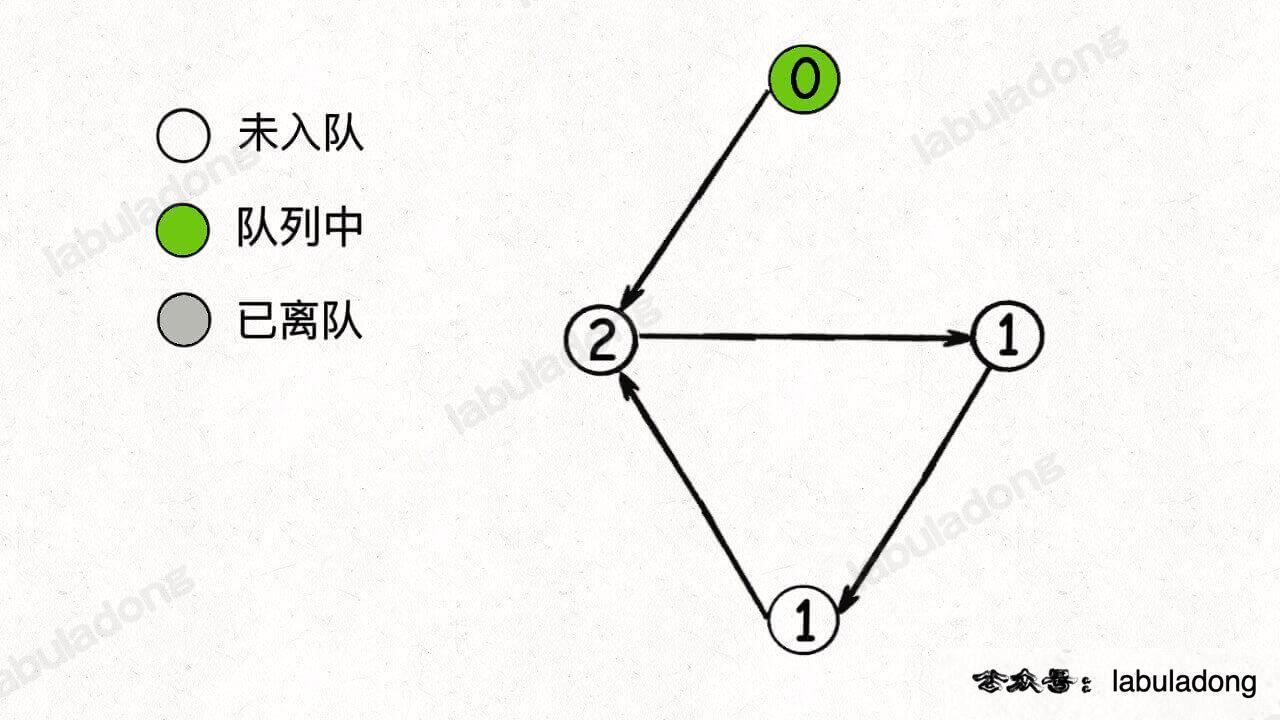
当弹出这个节点并减小相邻节点的入度之后队列为空,但并没有产生新的入度为 0 的节点加入队列,所以 BFS 算法终止:
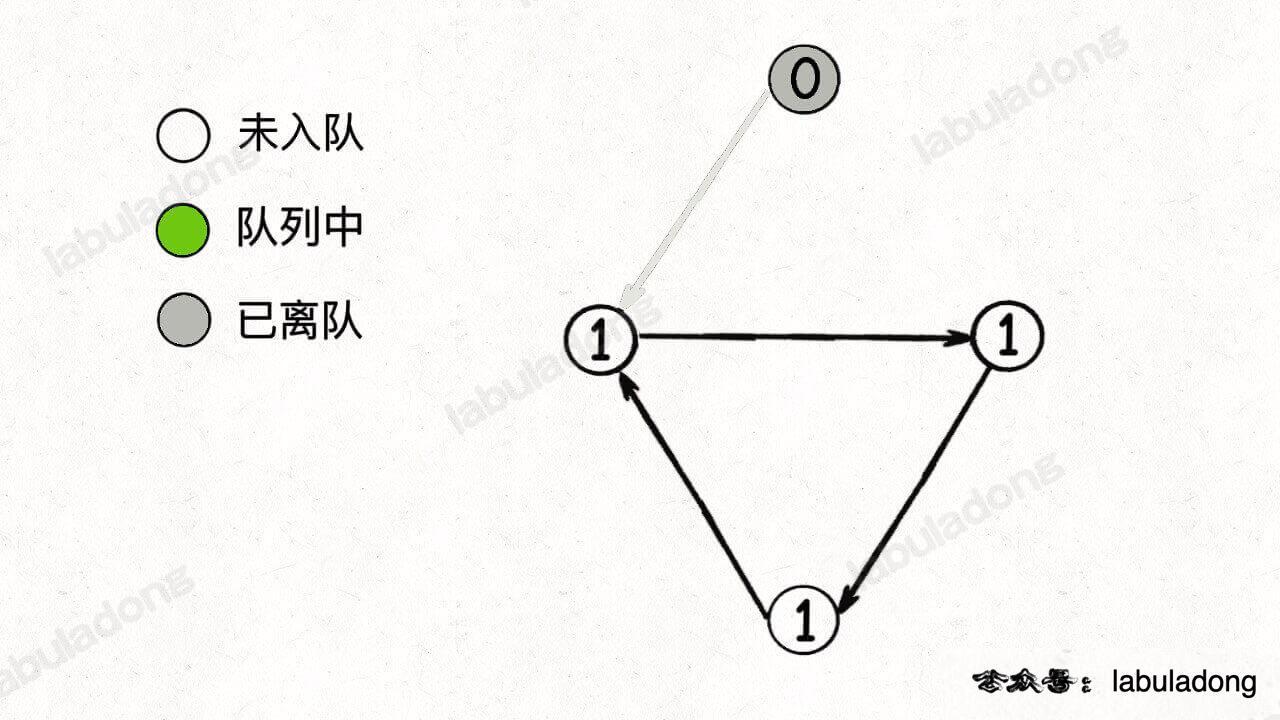
你看到了,如果存在节点没有被遍历,那么说明图中存在环,现在回头去看 BFS 的代码,你应该就很容易理解其中的逻辑了。
拓扑排序算法(BFS 版本)
如果你能看懂 BFS 版本的环检测算法,那么就很容易得到 BFS 版本的拓扑排序算法,因为节点的遍历顺序就是拓扑排序的结果。
比如刚才举的第一个例子,下图每个节点中的值即入队的顺序:
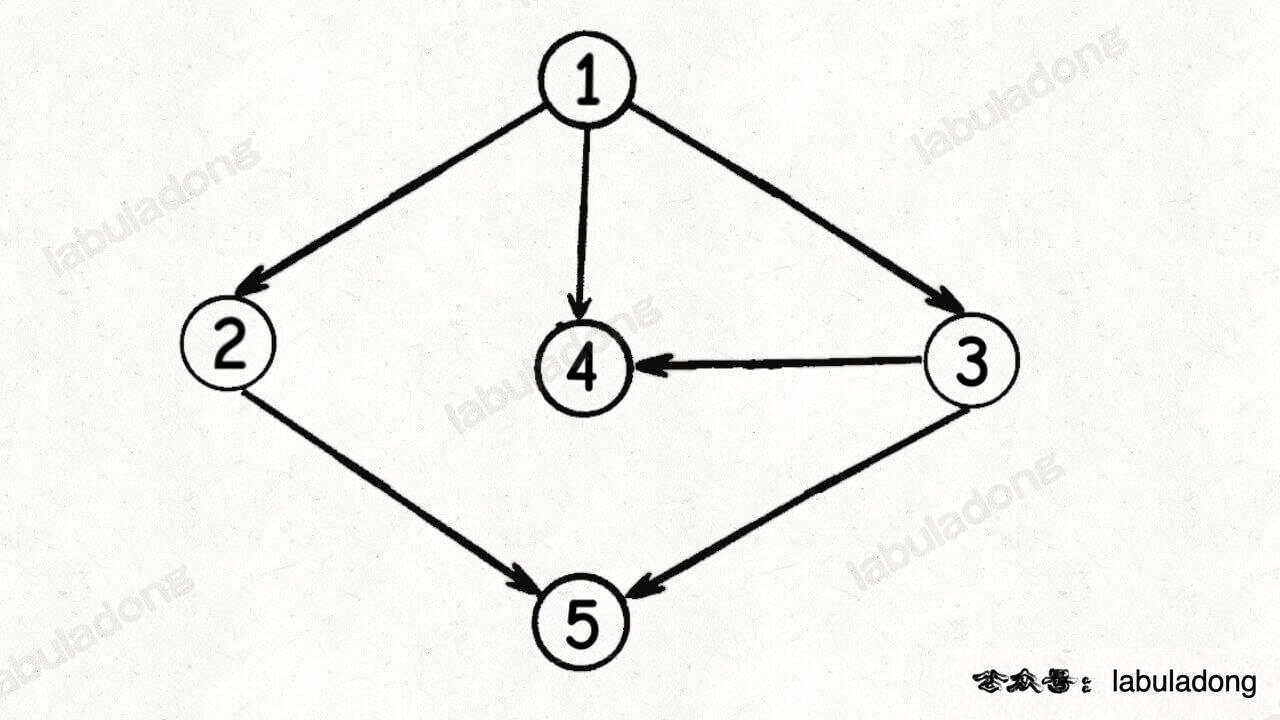
显然,这个顺序就是一个可行的拓扑排序结果。
所以,我们稍微修改一下 BFS 版本的环检测算法,记录节点的遍历顺序即可得到拓扑排序的结果:
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
// 建图,和环检测算法相同
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
// 计算入度,和环检测算法相同
int[] indegree = new int[numCourses];
for (int[] edge : prerequisites) {
int from = edge[1], to = edge[0];
indegree[to]++;
}
// 根据入度初始化队列中的节点,和环检测算法相同
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
// 记录拓扑排序结果
int[] res = new int[numCourses];
// 记录遍历节点的顺序(索引)
int count = 0;
// 开始执行 BFS 算法
while (!q.isEmpty()) {
int cur = q.poll();
// 弹出节点的顺序即为拓扑排序结果
res[count] = cur;
count++;
for (int next : graph[cur]) {
indegree[next]--;
if (indegree[next] == 0) {
q.offer(next);
}
}
}
if (count != numCourses) {
// 存在环,拓扑排序不存在
return new int[]{};
}
return res;
}
// 建图函数
List<Integer>[] buildGraph(int n, int[][] edges) {
// 见前文
}
}按道理,图的遍历 都需要 visited 数组防止走回头路,这里的 BFS 算法其实是通过 indegree 数组实现的 visited 数组的作用,只有入度为 0 的节点才能入队,从而保证不会出现死循环。
好了,到这里环检测算法、拓扑排序算法的 BFS 实现也讲完了,继续留一个思考题:
对于 BFS 的环检测算法,如果问你形成环的节点具体是哪些,你应该如何实现呢?
引用本文的文章
- [Kruskal 最小生成树算法](https://labuladong.online/algo/data-structure/kruskal/)
- [【强化练习】BFS 经典习题 I](https://labuladong.online/algo/problem-set/bfs/)
- [图结构基础及通用代码实现](https://labuladong.online/algo/data-structure-basic/graph-basic/)
- [图结构的 DFS/BFS 遍历](https://labuladong.online/algo/data-structure-basic/graph-traverse-basic/)
- [学习数据结构和算法的框架思维](https://labuladong.online/algo/essential-technique/algorithm-summary/)
- [用算法打败算法](https://labuladong.online/algo/fname.html?fname=PDF中的算法)