Union-Find 并查集算法

通知:为满足广大读者的需求,网站上架 速成目录,如有需要可以看下,谢谢大家的支持~另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
-----------
[!NOTE]
阅读本文前,你需要先学习:
并查集(Union-Find)算法是一个专门针对「动态连通性」的算法,我之前写过两次,因为这个算法的考察频率高,而且它也是最小生成树算法的前置知识,所以我整合了本文,争取一篇文章把这个算法讲明白。
首先,从什么是图的动态连通性开始讲。
一、动态连通性
简单说,动态连通性其实可以抽象成给一幅图连线。比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:
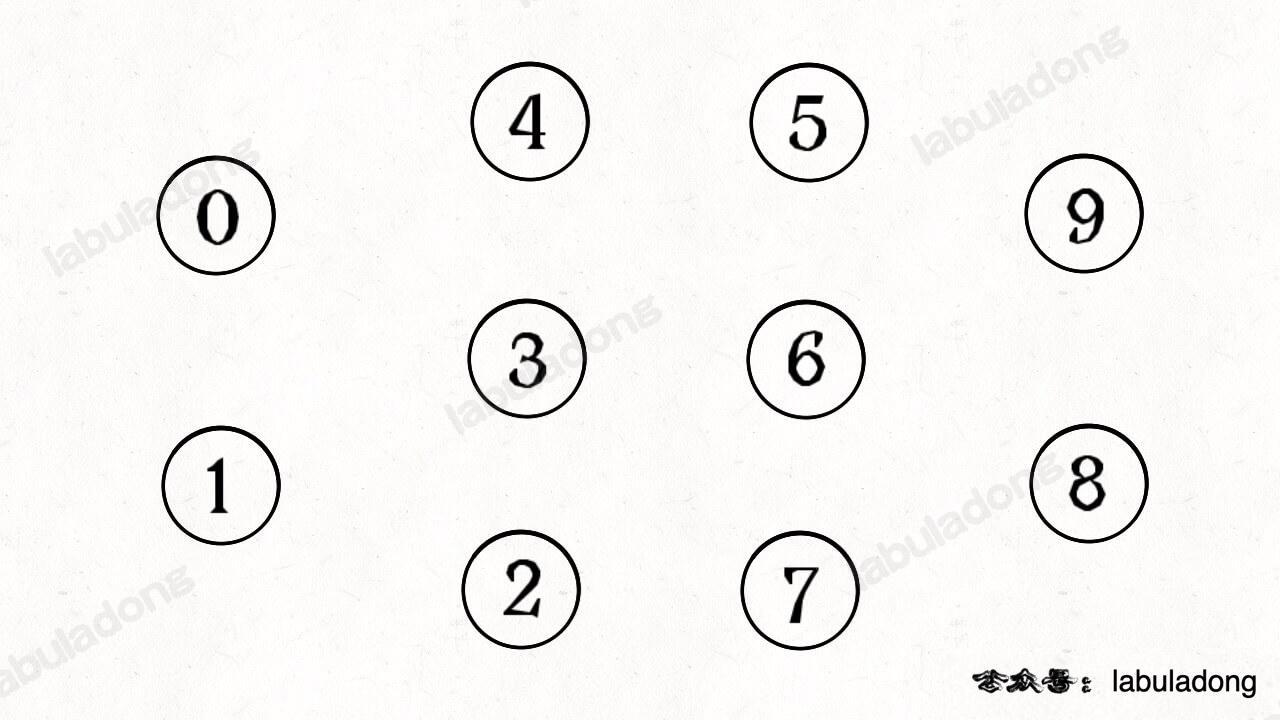
现在我们的 Union-Find 算法主要需要实现这两个 API:
class UF {
// 将 p 和 q 连接
public void union(int p, int q);
// 判断 p 和 q 是否连通
public boolean connected(int p, int q);
// 返回图中有多少个连通分量
public int count();
}这里所说的「连通」是一种等价关系,也就是说具有如下三个性质:
1、自反性:节点 p 和 p 是连通的。
2、对称性:如果节点 p 和 q 连通,那么 q 和 p 也连通。
3、传递性:如果节点 p 和 q 连通,q 和 r 连通,那么 p 和 r 也连通。
比如说之前那幅图,0~9 任意两个不同的点都不连通,调用 connected 都会返回 false,连通分量为 10 个。
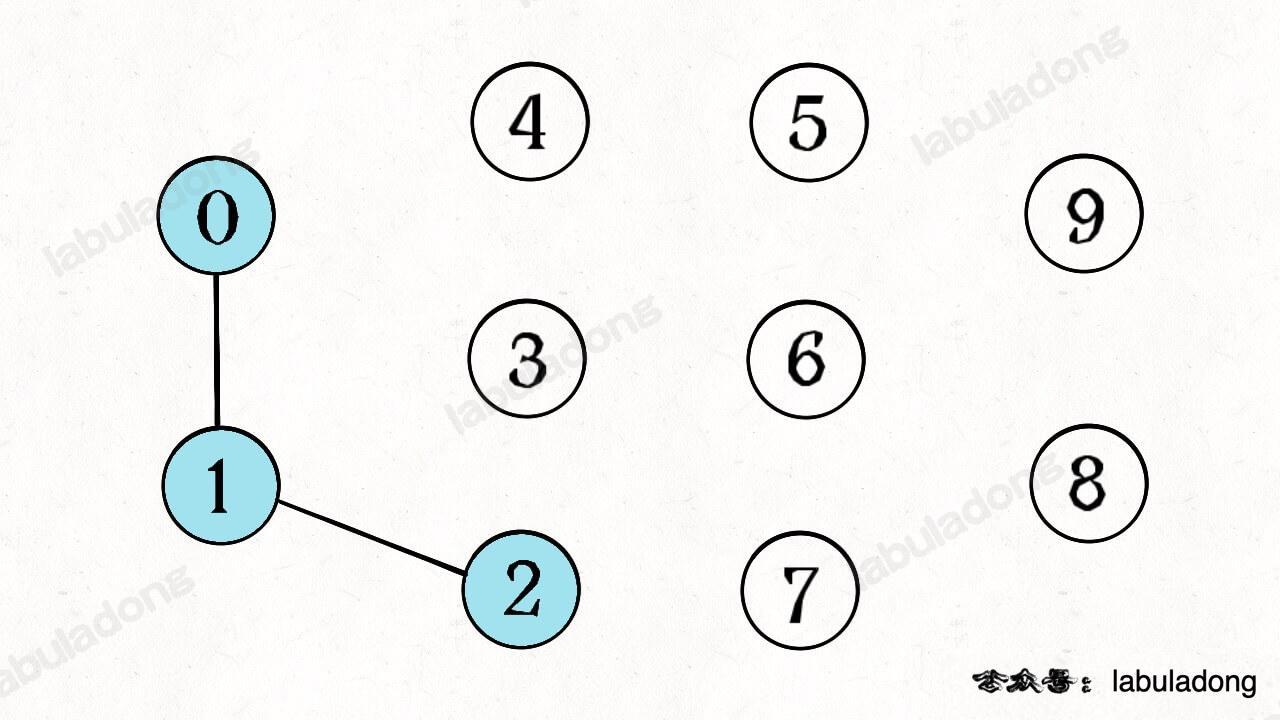
如果现在调用 union(0, 1),那么 0 和 1 被连通,连通分量降为 9 个。
再调用 union(1, 2),这时 0,1,2 都被连通,调用 connected(0, 2) 也会返回 true,连通分量变为 8 个。
判断这种「等价关系」非常实用,比如说编译器判断同一个变量的不同引用,比如社交网络中的朋友圈计算等等。
这样,你应该大概明白什么是动态连通性了,Union-Find 算法的关键就在于 union 和 connected 函数的效率。那么用什么模型来表示这幅图的连通状态呢?用什么数据结构来实现代码呢?
二、基本思路
注意我刚才把「模型」和具体的「数据结构」分开说,这么做是有原因的。因为我们使用森林(若干棵树)来表示图的动态连通性,用数组来具体实现这个森林。
怎么用森林来表示连通性呢?我们设定树的每个节点有一个指针指向其父节点,如果是根节点的话,这个指针指向自己。比如说刚才那幅 10 个节点的图,一开始的时候没有相互连通,就是这样:

class UF {
// 记录连通分量
private int count;
// 节点 x 的父节点是 parent[x]
private int[] parent;
// 构造函数,n 为图的节点总数
public UF(int n) {
// 一开始互不连通
this.count = n;
// 父节点指针初始指向自己
parent = new int[n];
for (int i = 0; i < n; i++)
parent[i] = i;
}
// 其他函数
}如果某两个节点被连通,则让其中的(任意)一个节点的根节点接到另一个节点的根节点上:

class UF {
// 为了节约篇幅,省略上文给出的代码部分...
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 将两棵树合并为一棵
parent[rootP] = rootQ;
// parent[rootQ] = rootP 也一样
// 两个分量合二为一
count--;
}
// 返回某个节点 x 的根节点
private int find(int x) {
// 根节点的 parent[x] == x
while (parent[x] != x)
x = parent[x];
return x;
}
// 返回当前的连通分量个数
public int count() {
return count;
}
}这样,如果节点 p 和 q 连通的话,它们一定拥有相同的根节点:

class UF {
// 为了节约篇幅,省略上文给出的代码部分...
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
}至此,Union-Find 算法就基本完成了。是不是很神奇?竟然可以这样使用数组来模拟出一个森林,如此巧妙的解决这个比较复杂的问题!
那么这个算法的复杂度是多少呢?我们发现,主要 API connected 和 union 中的复杂度都是 find 函数造成的,所以说它们的复杂度和 find 一样。
find 主要功能就是从某个节点向上遍历到树根,其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是 logN,但这并不一定。logN 的高度只存在于平衡二叉树,对于一般的树可能出现极端不平衡的情况,使得「树」几乎退化成「链表」,树的高度最坏情况下可能变成 N。

所以说上面这种解法,find , union , connected 的时间复杂度都是 O(N. 。这个复杂度很不理想的,你想图论解决的都是诸如社交网络这样数据规模巨大的问题,对于 ✅union 和 connected 的调用非常频繁,每次调用需要线性时间完全不可忍受。
问题的关键在于,如何想办法避免树的不平衡呢?只需要略施小计即可。
三、平衡性优化
我们要知道哪种情况下可能出现不平衡现象,关键在于 union 过程:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 将两棵树合并为一棵
parent[rootP] = rootQ;
// parent[rootQ] = rootP 也可以
count--;
}
}我们一开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下面,那么这里就可能出现「头重脚轻」的不平衡状况,比如下面这种局面:

长此以往,树可能生长得很不平衡。我们其实是希望,小一些的树接到大一些的树下面,这样就能避免头重脚轻,更平衡一些。解决方法是额外使用一个 size 数组,记录每棵树包含的节点数,我们不妨称为「重量」:
class UF {
private int count;
private int[] parent;
// 新增一个数组记录树的「重量」
private int[] size;
public UF(int n) {
this.count = n;
parent = new int[n];
// 最初每棵树只有一个节点
// 重量应该初始化 1
size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 其他函数
}比如说 size[3] = 5 表示,以节点 3 为根的那棵树,总共有 5 个节点。这样我们可以修改一下 union 方法:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 小树接到大树下面,较平衡
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
}这样,通过比较树的重量,就可以保证树的生长相对平衡,树的高度大致在 logN 这个数量级,极大提升执行效率。
此时,find , union , connected 的时间复杂度都下降为 O(logN),即便数据规模上亿,所需时间也非常少。
四、路径压缩
这步优化虽然代码很简单,但原理非常巧妙。
其实我们并不在乎每棵树的结构长什么样,只在乎根节点。
因为无论树长啥样,树上的每个节点的根节点都是相同的,所以能不能进一步压缩每棵树的高度,使树高始终保持为常数?

这样每个节点的父节点就是整棵树的根节点,find 就能以 O(1) 的时间找到某一节点的根节点,相应的,connected 和 union 复杂度都下降为 O(1)。
要做到这一点主要是修改 find 函数逻辑,非常简单,但你可能会看到两种不同的写法。
第一种是在 find 中加一行代码:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
private int find(int x) {
while (parent[x] != x) {
// 这行代码进行路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
}这个操作有点匪夷所思,看个 GIF 就明白它的作用了(为清晰起见,这棵树比较极端):

用语言描述就是,每次 while 循环都会让部分子节点向上移动,这样每次调用 find 函数向树根遍历的同时,顺手就将树高缩短了。
路径压缩的第二种写法是这样:
class UF {
// 为了节约篇幅,省略上文给出的代码部分...
// 第二种路径压缩的 find 方法
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
}我一度认为这种递归写法和第一种迭代写法做的事情一样,但实际上是我大意了,有读者指出这种写法进行路径压缩的效率是高于上一种解法的。
这个递归过程有点不好理解,你可以自己手画一下递归过程。我把这个函数做的事情翻译成迭代形式,方便你理解它进行路径压缩的原理:
// 这段迭代代码方便你理解递归代码所做的事情
public int find(int x) {
// 先找到根节点
int root = x;
while (parent[root] != root) {
root = parent[root];
}
// 然后把 x 到根节点之间的所有节点直接接到根节点下面
int old_parent = parent[x];
while (x != root) {
parent[x] = root;
x = old_parent;
old_parent = parent[old_parent];
}
return root;
}这种路径压缩的效果如下:

比起第一种路径压缩,显然这种方法压缩得更彻底,直接把一整条树枝压平,一点意外都没有。就算一些极端情况下产生了一棵比较高的树,只要一次路径压缩就能大幅降低树高,从 摊还分析 的角度来看,所有操作的平均时间复杂度依然是 O(1),所以从效率的角度来说,推荐你使用这种路径压缩算法。
另外,如果使用路径压缩技巧,那么 size 数组的平衡优化就没有必要了。所以你一般看到的 Union Find 算法应该是如下实现:
class UF {
// 连通分量个数
private int count;
// 存储每个节点的父节点
private int[] parent;
// n 为图中节点的个数
public UF(int n) {
this.count = n;
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// 将节点 p 和节点 q 连通
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
parent[rootQ] = rootP;
// 两个连通分量合并成一个连通分量
count--;
}
// 判断节点 p 和节点 q 是否连通
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// 返回图中的连通分量个数
public int count() {
return count;
}
}Union-Find 算法的复杂度可以这样分析:构造函数初始化数据结构需要 O(N. 的时间和空间复杂度;连通两个节点 ✅union、判断两个节点的连通性 connected、计算连通分量 count 所需的时间复杂度均为 O(1)。
到这里,相信你已经掌握了 Union-Find 算法的核心逻辑,总结一下我们优化算法的过程:
1、用 parent 数组记录每个节点的父节点,相当于指向父节点的指针,所以 parent 数组内实际存储着一个森林(若干棵多叉树)。
2、用 size 数组记录着每棵树的重量,目的是让 union 后树依然拥有平衡性,保证各个 API 时间复杂度为 O(logN),而不会退化成链表影响操作效率。
3、在 find 函数中进行路径压缩,保证任意树的高度保持在常数,使得各个 API 时间复杂度为 O(1)。使用了路径压缩之后,可以不使用 size 数组的平衡优化。
[!TIP]
大部分笔试都是允许你使用自己的 IDE 编码的,所以你可以提前把这个UF类用你熟悉的编程语言写好,笔试需要时直接拿来用。它的代码量稍微有点多,没必要现场从头写。
引用本文的文章
- [Kruskal 最小生成树算法](https://labuladong.online/algo/data-structure/kruskal/)
- [Prim 最小生成树算法](https://labuladong.online/algo/data-structure/prim/)
- [Union Find 并查集原理](https://labuladong.online/algo/data-structure-basic/union-find-basic/)
- [【强化练习】BFS 经典习题 II](https://labuladong.online/algo/problem-set/bfs-ii/)
- [【强化练习】并查集经典习题](https://labuladong.online/algo/problem-set/union-find/)
- [【强化练习】运用层序遍历解题 II](https://labuladong.online/algo/problem-set/binary-tree-level-ii/)
- [一文秒杀所有岛屿题目](https://labuladong.online/algo/frequency-interview/island-dfs-summary/)
- [二叉树基础及常见类型](https://labuladong.online/algo/data-structure-basic/binary-tree-basic/)
- [学习数据结构和算法的框架思维](https://labuladong.online/algo/essential-technique/algorithm-summary/)
- [用算法打败算法](https://labuladong.online/algo/fname.html?fname=PDF中的算法)