经典动态规划:编辑距离

通知:为满足广大读者的需求,网站上架 速成目录,如有需要可以看下,谢谢大家的支持~另外,建议你在我的 网站 学习文章,体验更好。
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 72. Edit Distance | 72. 编辑距离 | 🔴 |
-----------
[!NOTE]
阅读本文前,你需要先学习:tip:本文有视频版:编辑距离详解动态规划。建议关注我的 B 站账号,我会用视频领读的方式带大家学习那些稍有难度的算法技巧。
前几天看了一份鹅厂的面试题,算法部分大半是动态规划,最后一题就是写一个计算编辑距离的函数,今天就专门写一篇文章来探讨一下这个问题。
力扣第 72 题「编辑距离」就是这个问题,先看下题目:
// 函数签名如下
int minDistance(String s1, String s2)对于没有接触过动态规划问题的读者来说,这道题还是有一定难度的,是不是感觉完全无从下手?
但这个问题本身还是比较实用的,我曾经就在日常生活中用到过这个算法。之前有一篇公众号文章由于疏忽,写错位了一段内容,我决定修改这部分内容让逻辑通顺。但是公众号文章最多只能修改 20 个字,且只支持增、删、替换操作(跟编辑距离问题一模一样),于是我就用算法求出了一个最优方案,只用了 16 步就完成了修改。
再比如高大上一点的应用,DNA 序列是由 A,G,C,T 组成的序列,可以类比成字符串。编辑距离可以衡量两个 DNA 序列的相似度,编辑距离越小,说明这两段 DNA 越相似,说不定这俩 DNA 的主人是远古近亲啥的。
下面言归正传,详细讲解一下编辑距离该怎么算,相信本文会让你有收获。
一、思路
编辑距离问题就是给我们两个字符串 s1 和 s2,只能用三种操作,让我们把 s1 变成 s2,求最少的操作数。需要明确的是,不管是把 s1 变成 s2 还是反过来,结果都是一样的,所以后文就以 s1 变成 s2 举例。
[!TIP]
解决两个字符串的动态规划问题,一般都是用两个指针i, j分别指向两个字符串的头部或尾部,然后尝试写状态转移方程。比方说让
i, j分别指向两个字符串的尾部,把dp[i], dp[j]定义为s1[0..i], s2[0..j]子串的编辑距离,那么i, j一步步往前移动的过程,就是问题规模(子串长度)逐步减小的过程。当然,你想让让
i, j分别指向字符串头部,然后一步步往后移动也可以,本质上并无区别,只要改一下dp函数/数组的定义即可。
设两个字符串分别为 "rad" 和 "apple",让 i, j 两个指针分别指向 s1, s2 的尾部,为了把 s1 变成 s2,算法会这样进行:

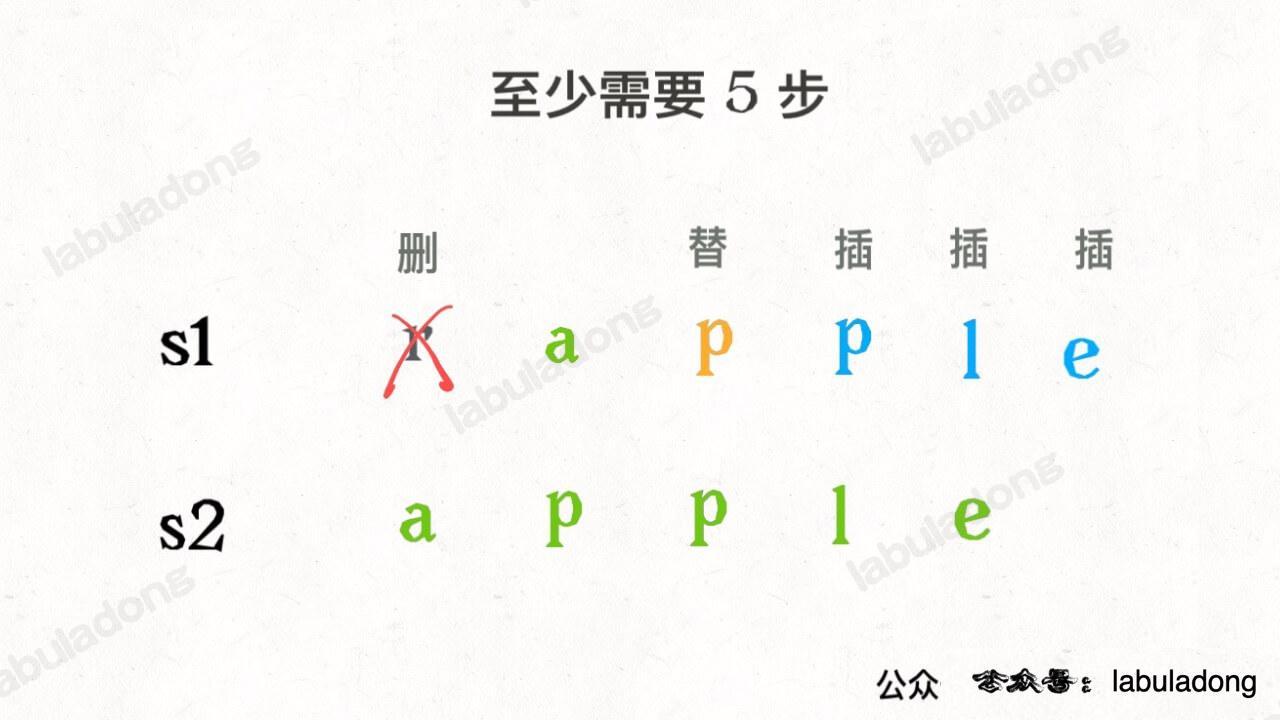
请记住这个 GIF 过程,这样就能算出编辑距离。关键在于如何做出正确的操作,稍后会讲。
根据上面的 GIF,可以发现操作不只有三个,其实还有第四个操作,就是什么都不要做(skip)。比如这个情况:

因为这两个字符本来就相同,为了使编辑距离最小,显然不应该对它们有任何操作,直接往前移动 i, j 即可。
还有一个很容易处理的情况,就是 j 走完 s2 时,如果 i 还没走完 s1,那么只能用删除操作把 s1 缩短为 s2。比如这个情况:
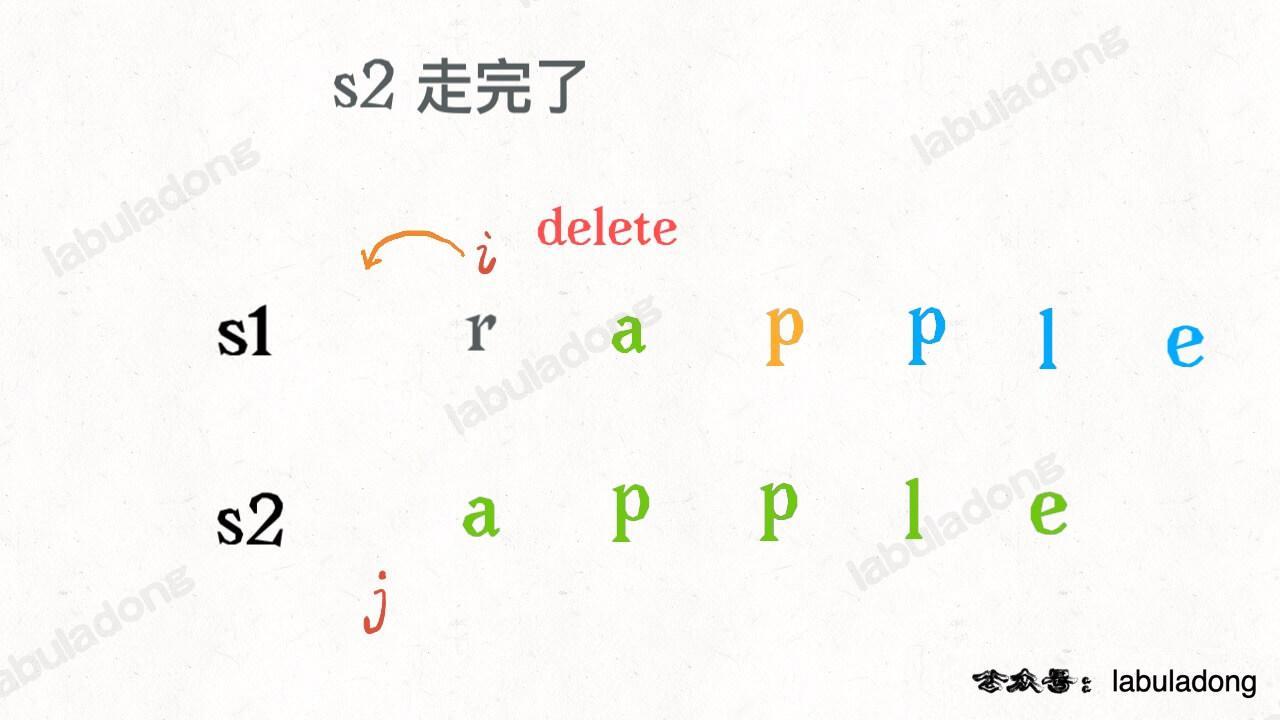
类似的,如果 i 走完 s1 时 j 还没走完了 s2,那就只能用插入操作把 s2 剩下的字符全部插入 s1。等会会看到,这两种情况就是算法的 base case。
下面详解一下如何将思路转换成代码。
二、代码详解
先梳理一下之前的思路:
base case 是 i 走完 s1 或 j 走完 s2,可以直接返回另一个字符串剩下的长度。
对于每对儿字符 s1[i] 和 s2[j],可以有四种操作:
if s1[i] == s2[j]:
啥都别做(skip)
i, j 同时向前移动
else:
三选一:
插入(insert)
删除(delete)
替换(replace)有这个框架,问题就已经解决了。读者也许会问,这个「三选一」到底该怎么选择呢?很简单,全试一遍,哪个操作最后得到的编辑距离最小,就选谁。这里需要递归技巧,先看下暴力解法代码:
class Solution {
public int minDistance(String s1, String s2) {
int m = s1.length(), n = s2.length();
// i,j 初始化指向最后一个索引
return dp(s1, m - 1, s2, n - 1);
}
// 定义:返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
int dp(String s1, int i, String s2, int j) {
// base case
if (i == -1) return j + 1;
if (j == -1) return i + 1;
if (s1.charAt(i) == s2.charAt(j)) {
// 啥都不做
return dp(s1, i - 1, s2, j - 1);
}
return min(
// 插入
dp(s1, i, s2, j - 1) + 1,
// 删除
dp(s1, i - 1, s2, j) + 1,
// 替换
dp(s1, i - 1, s2, j - 1) + 1
);
}
int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
}下面来详细解释一下这段递归代码,base case 应该不用解释了,主要解释一下递归部分。
都说递归代码的可解释性很好,这是有道理的,只要理解函数的定义,就能很清楚地理解算法的逻辑。我们这里 dp 函数的定义是这样的:
// 定义:返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
int dp(String s1, int i, String s2, int j)记住这个定义之后,先来看这段代码:
if s1[i] == s2[j]:
# 啥都不做
return dp(s1, i - 1, s2, j - 1)
# 解释:
# 本来就相等,不需要任何操作
# s1[0..i] 和 s2[0..j] 的最小编辑距离等于
# s1[0..i-1] 和 s2[0..j-1] 的最小编辑距离
# 也就是说 dp(i, j) 等于 dp(i-1, j-1)如果 s1[i] != s2[j],就要对三个操作递归了,稍微需要点思考:
# 插入
dp(s1, i, s2, j - 1) + 1,
# 解释:
# 我直接在 s1[i] 插入一个和 s2[j] 一样的字符
# 那么 s2[j] 就被匹配了,前移 j,继续跟 i 对比
# 别忘了操作数加一
# 删除
dp(s1, i - 1, s2, j) + 1,
# 解释:
# 我直接把 s[i] 这个字符删掉
# 前移 i,继续跟 j 对比
# 操作数加一
# 替换
dp(s1, i - 1, s2, j - 1) + 1
# 解释:
# 我直接把 s1[i] 替换成 s2[j],这样它俩就匹配了
# 同时前移 i,j 继续对比
# 操作数加一
现在,你应该完全理解这段短小精悍的代码了。还有点小问题就是,这个解法是暴力解法,存在重叠子问题,需要用动态规划技巧来优化。
怎么能一眼看出存在重叠子问题呢?我在 动态规划答疑篇 有讲过,这里再简单提一下,需要抽象出本文算法的递归框架:
int dp(i, j) {
dp(i - 1, j - 1); // #1
dp(i, j - 1); // #2
dp(i - 1, j); // #3
}对于子问题 dp(i-1, j-1),如何通过原问题 dp(i, j) 得到呢?有不止一条路径,比如 dp(i, j) -> #1 和 dp(i, j) -> #2 -> #3。一旦发现一条重复路径,就说明存在巨量重复路径,也就是重叠子问题。
三、动态规划优化
对于重叠子问题呢,前文 动态规划详解 详细介绍过,优化方法无非是给递归解法加备忘录,或者把动态规划过程用 DP table 迭代实现,下面逐个来讲。
备忘录解法
既然暴力递归解法都写出来了,备忘录是很容易加的,原来的代码稍加修改即可:
class Solution {
// 备忘录
int[][] memo;
public int minDistance(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 备忘录初始化为特殊值,代表还未计算
memo = new int[m][n];
for (int[] row : memo) {
Arrays.fill(row, -1);
}
return dp(s1, m - 1, s2, n - 1);
}
int dp(String s1, int i, String s2, int j) {
if (i == -1) return j + 1;
if (j == -1) return i + 1;
// 查备忘录,避免重叠子问题
if (memo[i][j] != -1) {
return memo[i][j];
}
// 状态转移,结果存入备忘录
if (s1.charAt(i) == s2.charAt(j)) {
memo[i][j] = dp(s1, i - 1, s2, j - 1);
} else {
memo[i][j] = min(
dp(s1, i, s2, j - 1) + 1,
dp(s1, i - 1, s2, j) + 1,
dp(s1, i - 1, s2, j - 1) + 1
);
}
return memo[i][j];
}
int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
}DP table 解法
主要说下 DP table 的解法,我们需要定义一个 dp 数组,然后在这个数组上执行状态转移方程。
首先明确 dp 数组的含义,由于本题有两个状态(索引 i 和 j),所以dp 数组是一个二维数组,大概长这样:
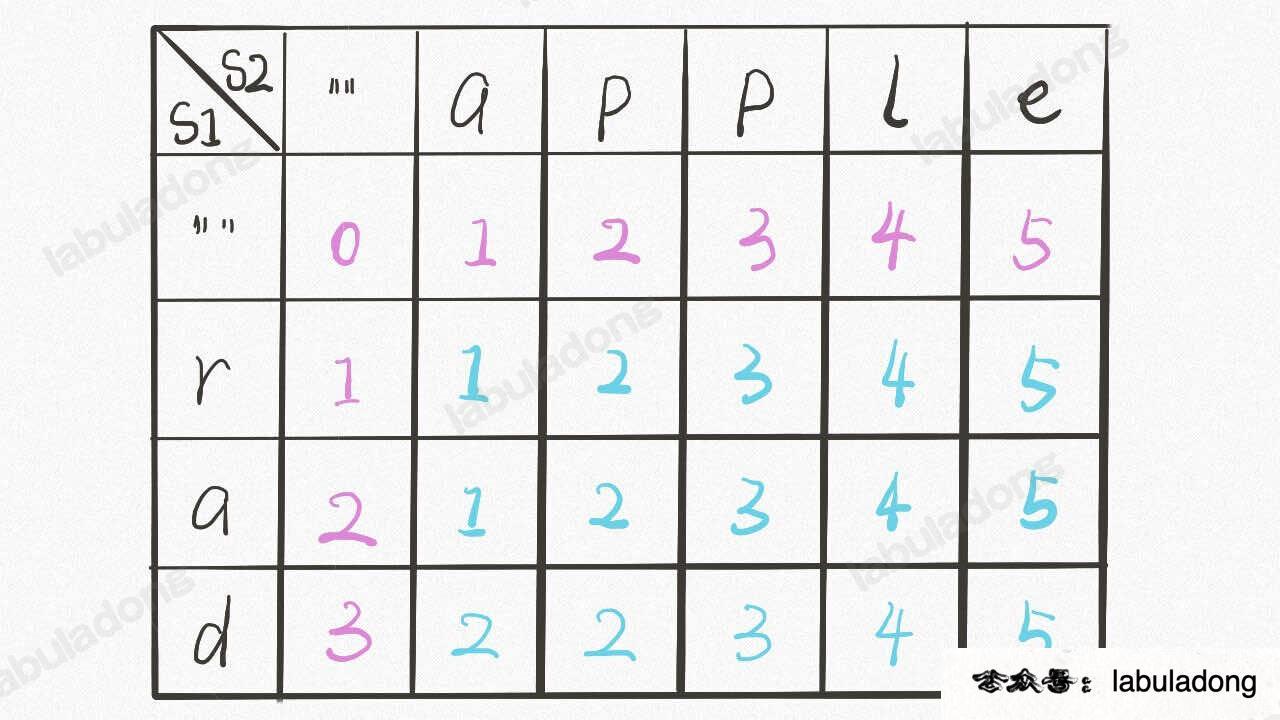
状态转移和递归解法相同,dp[..][0] 和 dp[0][..] 对应 base case,dp[i][j] 的含义和之前 dp 函数的定义类似:
int dp(String s1, int i, String s2, int j)
// 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
dp[i-1][j-1]
// 存储 s1[0..i] 和 s2[0..j] 的最小编辑距离dp 函数的 base case 是 i, j 等于 -1,而数组索引至少是 0,所以 dp 数组会偏移一位。
既然 dp 数组和递归 dp 函数含义一样,也就可以直接套用之前的思路写代码,唯一不同的是,递归解法是自顶向下求解(从原问题开始,逐步分解到 base case),DP table 是自底向上求解(从 base case 开始,向原问题推演):
class Solution {
public int minDistance(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp[i+1][j+1]
int[][] dp = new int[m + 1][n + 1];
// base case
for (int i = 1; i <= m; i++)
dp[i][0] = i;
for (int j = 1; j <= n; j++)
dp[0][j] = j;
// 自底向上求解
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (s1.charAt(i-1) == s2.charAt(j-1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = min(
dp[i - 1][j] + 1,
dp[i][j - 1] + 1,
dp[i - 1][j - 1] + 1
);
}
}
}
// 储存着整个 s1 和 s2 的最小编辑距离
return dp[m][n];
}
int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
}
🎃 代码可视化动画🎃
四、扩展延伸
一般来说,处理两个字符串的动态规划问题,都是按本文的思路处理,建立 DP table。为什么呢,因为易于找出状态转移的关系,比如编辑距离的 DP table:

还有一个细节,既然每个 dp[i][j] 只和它附近的三个状态有关,空间复杂度是可以压缩成 $O(min(M, N. )$ 的(M,N 是两个字符串的长度)。不难,但是可解释性大大降低,读者可以自己尝试优化一下。✅
你可能还会问,这里只求出了最小的编辑距离,那具体的操作是什么?你之前举的修改公众号文章的例子,只有一个最小编辑距离肯定不够,还得知道具体怎么修改才行。
这个其实很简单,代码稍加修改,给 dp 数组增加额外的信息即可:
// int[][] dp;
Node[][] dp;
class Node {
int val;
int choice;
// 0 代表啥都不做
// 1 代表插入
// 2 代表删除
// 3 代表替换
}val 属性就是之前的 dp 数组的数值,choice 属性代表操作。在做最优选择时,顺便把操作记录下来,然后就从结果反推具体操作。
我们的最终结果不是 dp[m][n] 吗,这里的 val 存着最小编辑距离,choice 存着最后一个操作,比如说是插入操作,那么就可以左移一格:
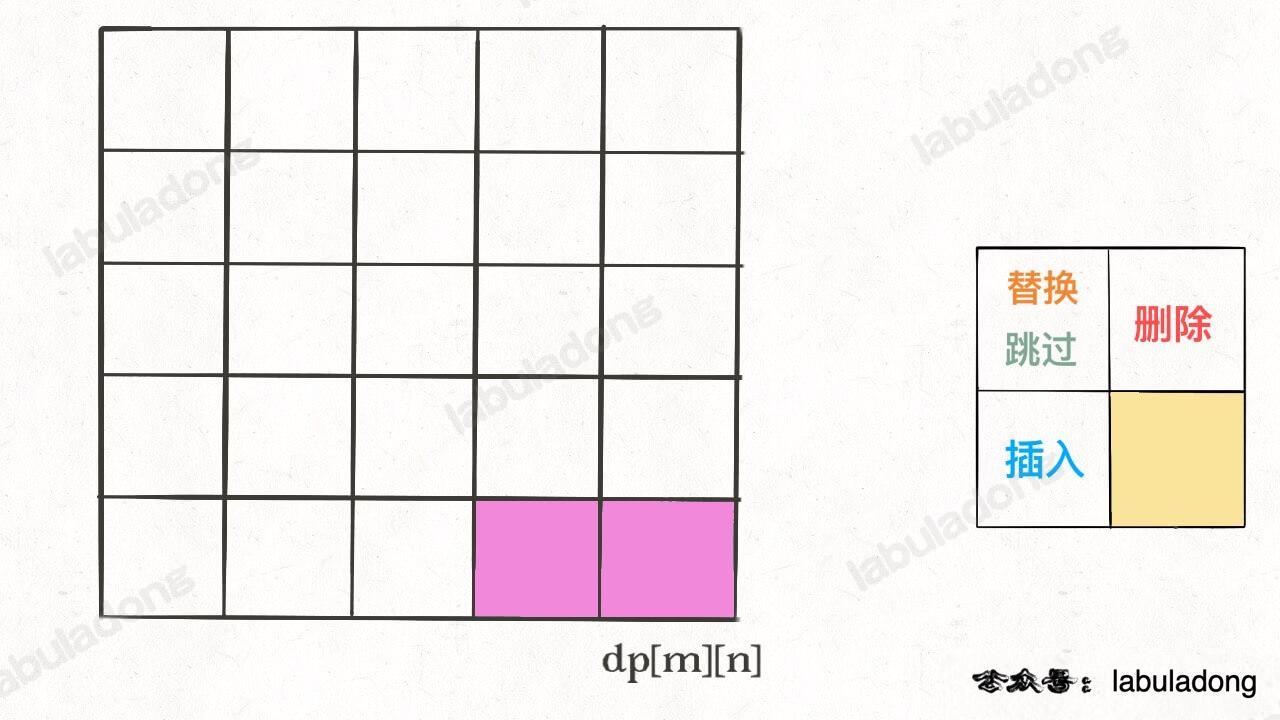
重复此过程,可以一步步回到起点 dp[0][0],形成一条路径,按这条路径上的操作进行编辑,就是最佳方案。
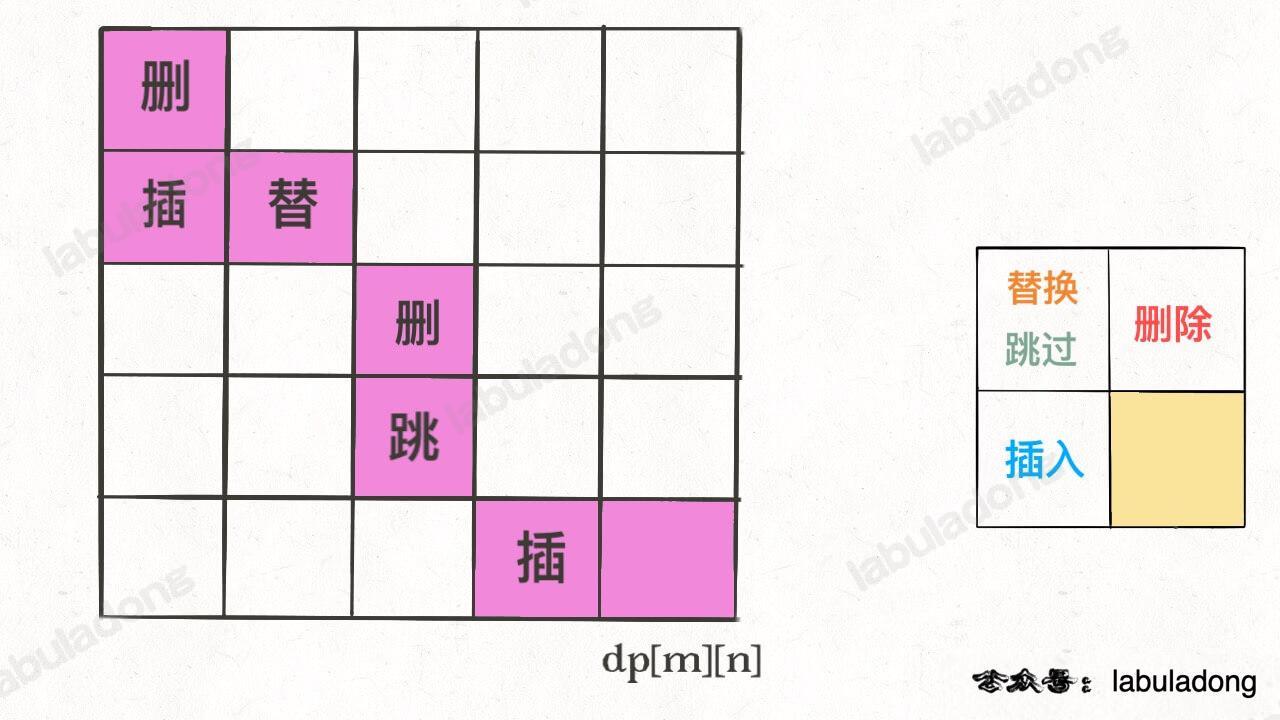
应大家的要求,我把这个思路也写出来,你可以自己运行试一下:
int minDistance(String s1, String s2) {
int m = s1.length(), n = s2.length();
Node[][] dp = new Node[m + 1][n + 1];
// base case
for (int i = 0; i <= m; i++) {
// s1 转化成 s2 只需要删除一个字符
dp[i][0] = new Node(i, 2);
}
for (int j = 1; j <= n; j++) {
// s1 转化成 s2 只需要插入一个字符
dp[0][j] = new Node(j, 1);
}
// 状态转移方程
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (s1.charAt(i-1) == s2.charAt(j-1)){
// 如果两个字符相同,则什么都不需要做
Node node = dp[i - 1][j - 1];
dp[i][j] = new Node(node.val, 0);
} else {
// 否则,记录代价最小的操作
dp[i][j] = minNode(
dp[i - 1][j],
dp[i][j - 1],
dp[i-1][j-1]
);
// 并且将编辑距离加一
dp[i][j].val++;
}
}
}
// 根据 dp table 反推具体操作过程并打印
printResult(dp, s1, s2);
return dp[m][n].val;
}
// 计算 delete, insert, replace 中代价最小的操作
Node minNode(Node a, Node b, Node c) {
Node res = new Node(a.val, 2);
if (res.val > b.val) {
res.val = b.val;
res.choice = 1;
}
if (res.val > c.val) {
res.val = c.val;
res.choice = 3;
}
return res;
}最后,printResult 函数反推结果并把具体的操作打印出来:
void printResult(Node[][] dp, String s1, String s2) {
int rows = dp.length;
int cols = dp[0].length;
int i = rows - 1, j = cols - 1;
System.out.println("Change s1=" + s1 + " to s2=" + s2 + ":n");
while (i != 0 && j != 0) {
char c1 = s1.charAt(i - 1);
char c2 = s2.charAt(j - 1);
int choice = dp[i][j].choice;
System.out.print("s1[" + (i - 1) + "]:");
switch (choice) {
case 0:
// 跳过,则两个指针同时前进
System.out.println("skip '" + c1 + "'");
i--; j--;
break;
case 1:
// 将 s2[j] 插入 s1[i],则 s2 指针前进
System.out.println("insert '" + c2 + "'");
j--;
break;
case 2:
// 将 s1[i] 删除,则 s1 指针前进
System.out.println("delete '" + c1 + "'");
i--;
break;
case 3:
// 将 s1[i] 替换成 s2[j],则两个指针同时前进
System.out.println(
"replace '" + c1 + "'" + " with '" + c2 + "'");
i--; j--;
break;
}
}
// 如果 s1 还没有走完,则剩下的都是需要删除的
while (i > 0) {
System.out.print("s1[" + (i - 1) + "]:");
System.out.println("delete '" + s1.charAt(i - 1) + "'");
i--;
}
// 如果 s2 还没有走完,则剩下的都是需要插入 s1 的
while (j > 0) {
System.out.print("s1[0]:");
System.out.println("insert '" + s2.charAt(j - 1) + "'");
j--;
}
}引用本文的文章
- [动态规划之子序列问题解题模板](https://labuladong.online/algo/dynamic-programming/subsequence-problem/)
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.online/algo/dynamic-programming/faq-summary/)
- [经典动态规划:正则表达式](https://labuladong.online/algo/dynamic-programming/regular-expression-matching/)