《思维的压缩艺术：CODI如何将链式思考浓缩为连续空间》

🧠 引言：当思维不再需要语言的束缚

想象一下，如果我们的大脑在解决复杂问题时，不必将每一步思考过程都转化为语言，而是直接在神经元之间传递抽象的信息。这种思维方式不仅更高效，还能避免语言表达带来的限制。在人工智能领域，一项名为CODI（Continuous Chain-of-Thought via Self-Distillation）的创新技术正在实现这一愿景，它让大型语言模型（LLMs）能够在连续空间中进行推理，而不必生成冗长的中间步骤文本。

近期由伦敦国王学院和艾伦图灵研究所的研究团队发表的这项研究，不仅在理论上提出了一种全新的思维范式，更在实践中证明了其惊人的效果。CODI首次实现了隐式链式思考（Implicit Chain-of-Thought）与显式链式思考（Explicit Chain-of-Thought）相当的性能，同时将推理过程压缩了3.1倍，大幅提升了推理效率。

让我们一起深入探索这项突破性技术背后的原理、创新点以及它对AI推理能力的深远影响。

🔍 背景：链式思考的困境与挑战

链式思考（Chain-of-Thought，简称CoT）是近年来大型语言模型实现复杂推理的关键技术。通过生成自然语言形式的中间推理步骤，模型能够像人类一样，一步步解决复杂问题。然而，这种方法存在两个根本性问题：

1. 自然语言可能不是推理的最佳媒介：神经科学研究表明，人类进行数学推理时，大脑中主要活跃的并非语言处理区域。这暗示自然语言可能不是进行推理的最优载体。
2. 推理效率低下：生成详细的推理步骤需要大量的计算资源和时间，特别是在处理复杂问题时，这种低效更为明显。

为解决这些问题，研究人员提出了隐式链式思考（Implicit CoT）的概念，旨在让模型无需生成显式的中间步骤文本，直接在内部表示空间中进行推理。然而，现有的隐式CoT方法，如iCoT和Coconut，虽然比不使用CoT的基线模型表现更好，但仍然显著落后于显式CoT方法。

🧩 核心挑战：如何在不生成显式CoT文本的情况下，让模型学会在连续空间中进行高效推理？

🌟 CODI：连续空间中的思维革命

🔮 核心理念：自蒸馏框架

CODI的核心创新在于提出了一种自蒸馏（Self-Distillation）框架，使同一个模型同时扮演”教师”和”学生”两种角色：

• 教师任务：学习生成显式CoT，掌握结构化的推理模式
• 学生任务：学习在连续空间中生成隐式CoT，无需生成中间文本步骤

通过这种设计，CODI实现了知识从显式CoT到隐式CoT的有效迁移，让模型能够在连续空间中进行高效推理。

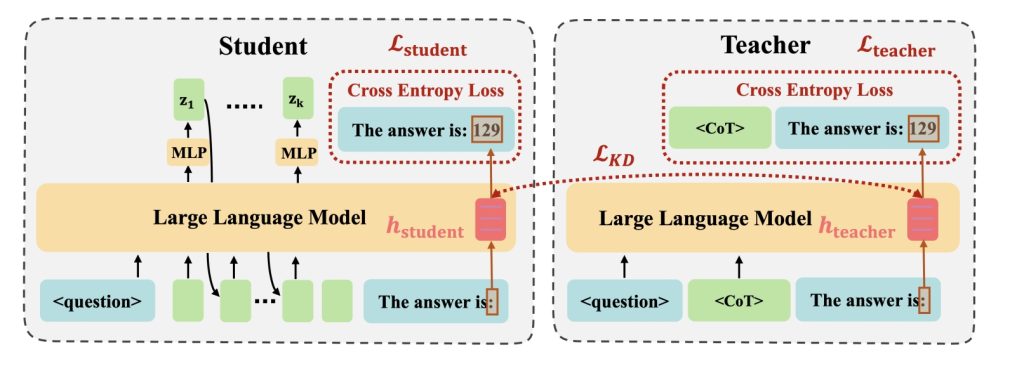
🧪 技术创新：隐藏激活对齐

CODI的关键技术创新在于识别并利用了一个重要发现：在生成最终答案的前一个token（通常是冒号”:”）的隐藏激活值中，包含了整个推理过程的关键信息。

研究者通过理论分析证明，CoT对这个token的隐藏激活值的影响主要表现为一个”位移”（shift）：

   

其中，$h^l_{CoT}$是使用CoT时第l层的隐藏激活值，$h^l_{no-CoT}$是不使用CoT时的对应激活值，而剩余项则量化了CoT推理R引入的位移。

基于这一发现，CODI通过L1距离损失函数，将学生任务中这个关键token的隐藏激活值与教师任务中对应token的隐藏激活值对齐：

   

这种对齐机制使得学生任务能够有效地学习到教师任务中蕴含的推理能力，而无需生成显式的CoT文本。

🔄 训练与推理过程

训练过程：

1. 教师任务通过语言建模目标学习生成显式CoT
2. 学生任务学习生成连续思考，并通过自回归方式传播隐藏状态
3. 通过L1距离损失函数，将学生和教师在关键token上的隐藏激活值对齐

推理过程：

1. 模型接收问题输入后，自回归地解码n个连续思考token
2. 推理完成后，插入eot（end-of-thought）token，切换到语言生成模式
3. 模型直接生成最终答案，无需生成中间推理步骤文本

📊 实验结果：压缩思维的惊人效果

🎯 数学推理性能

在GSM8k数学推理基准测试上，CODI取得了令人瞩目的成绩：

• 使用GPT-2模型时，CODI达到了43.7%的准确率，比iCoT高出45.7%，比Coconut高出28.2%
• CODI是首个性能与显式CoT相当的隐式CoT方法，达到了CoT-SFT性能的99.1%
• 在LLaMA3.2-1b模型上，CODI同样表现出色，达到了CoT-SFT性能的90.3%

⚡ 效率提升

CODI使用固定的6个连续思考token（加上2个特殊token，共8个token）进行推理，相比显式CoT方法：

• 对于简洁CoT（GSM8k-Aug数据集），实现了约2.7倍的速度提升（3.1倍的CoT压缩率）
• 对于冗长CoT（GSM8k-Aug-NL数据集），实现了约5.9倍的速度提升（7.8倍的CoT压缩率）

🛡️ 鲁棒性与泛化能力

CODI在多个领域外（Out-of-Distribution）数据集上表现出色：

• 在SVAMP、GSM-Hard和MultiArith三个基准测试上，CODI使用GPT-2模型时甚至超过了CoT-SFT
• 这种优势可能源于CODI较低的过拟合倾向，因为它在训练过程中没有确切的模仿目标

📈 压缩比率分析

研究者还探索了不同数量连续思考token对性能的影响：

• CODI在所有压缩比率下都优于Coconut
• 两种方法都在使用6个连续思考token时达到性能峰值
• 这可能与数据集结构有关，特别是平均CoT步骤数

🔬 深入分析：连续思维的可解释性

尽管CODI的连续思考缺乏显式的模仿目标，但研究者发现它具有令人惊讶的可解释性。通过将连续思考的最后隐藏状态投影到词汇空间，可以观察到CODI能够产生可观察的中间结果。

在上图的案例中，我们可以看到：

1. 第二个思考token（z2）关注”1″和”7″，产生解码token”7″
2. 中间结果之间由看似无意义的连续token分隔，可能作为计算中间结果的过渡状态
3. 通过分析注意力机制，可以推断变压器层隐式执行数学运算

研究者还通过准确率指标验证了CODI可解释性的普遍性：

• 当只有一个中间结果时，CODI正确匹配参考结果的准确率达97.1%
• 对于长度达3的CoT序列，CODI在解码有效中间结果方面的准确率仍超过75%

这些发现表明，CODI不仅能够在连续空间中高效推理，还能保持推理过程的可解释性，这对于构建可信赖的AI系统至关重要。

🧩 CODI的模式学习

研究者还探索了一个有趣的问题：CODI是否等同于在包含其解码模式的数据集上微调的GPT-2？

为此，他们创建了两个合成数据集：

1. 仅包含中间结果的数据集（例如：”CoT: 20, 7, 27. Result: 9″）
2. 包含运算符和结果的数据集（例如：”CoT: ×, 20, ×, 7, +, 27. Result: 9″）

实验结果表明，虽然在这两个合成数据集上训练的模型优于No-CoT基线，但它们的性能显著低于CoT和CODI，仅与Coconut相当。这表明CODI通过蒸馏从教师任务中学习到的信息比纯粹在语言层面上模仿中间结果更丰富，突显了CODI训练框架的优势。

🔮 未来展望与局限性

尽管CODI取得了显著成功，但研究者也指出了几个局限性和未来研究方向：

1. 蒸馏token选择：当前方法专注于探测负责生成第一个答案token的token（”:”），但这可能不是最优选择。探索其他可能的蒸馏token可能进一步提升性能。
2. 优化挑战：当前连续训练方法缺乏中间梯度，直到序列结束才有梯度。这可能导致优化挑战，特别是在扩展到需要更长连续推理链的复杂问题时。
3. 确定性推理：CODI当前配置是完全确定性的，而CoT的一个优势是其内在的随机性，允许模型通过自一致性、树搜索等方法提高性能。引入可控的随机性可能恢复这一特性。
4. 领域扩展：当前研究主要集中在数学问题上，未来工作应探索CODI在更广泛推理场景中的适用性。

🌐 结论：思维压缩的新范式

CODI代表了AI推理能力的一个重要突破，它证明了在连续空间中进行推理不仅可行，而且能够达到与显式CoT相当的性能，同时显著提高效率。这一发现挑战了传统观念，表明自然语言可能不是推理的最佳媒介，而更紧凑的连续表示可能更适合捕捉推理的抽象本质。

通过创新的自蒸馏框架和隐藏激活对齐机制，CODI成功地将显式CoT的知识转移到隐式CoT中，实现了思维的有效压缩。这不仅提高了推理效率，还保持了推理过程的可解释性，为构建更高效、更可信赖的AI系统开辟了新途径。

随着研究的深入，我们可以期待CODI在更多样化和具有挑战性的任务中的应用，以及与多模态等技术的集成，为AI推理能力的发展带来更多可能性。

📚 参考文献

1. Shen, Z. , Yan, H., Zhang, L., Hu, Z., Du, Y., & He, Y. (2024). CODI: Compressing Chain-of-Thought into Continuous Space via Self-Distillation. arXiv:2502.21074.✅
2. Wei, J. , Wang, X., Schuurmans, D., Bosma, M., Ichter, B., Xia, F., … & Zhou, D. (2022). Chain-of-thought prompting elicits reasoning in large language models. Advances in Neural Information Processing Systems, 35.✅
3. Hao, Y. , Dong, L., Xia, F., & Wei, J. (2024). Coconut: Training-Free Continuous Chain-of-Thought Reasoning. arXiv preprint.✅
4. Deng, X. , Khattab, G., Yu, A. W., Saunshi, N., Arora, S., & Zaharia, M. (2024). Implicit Chain of Thought Reasoning via Knowledge Distillation. arXiv preprint.✅
5. Orgad, M. , Riddell, A., Frankle, J., Stoica, I., & Carbin, M. (2025). Attention Satisfies: A Constraint-Satisfaction Lens on Factual Errors of Language Models. arXiv preprint.✅