基于饱和数学的一些解题技巧

在传统的数学教育里，1/0是万万使不得的。

但，我们可以定义 1/0= 10000，而无穷小=0.00001。

以上就是一种饱和数学的思想，有一个数学分支叫非标数学分析。

在传统极限理论中，我们有

$\lim_{x\to+\infty}\frac{\sin x}{x}=0$

这是利用分母 $x$ 趋向无穷大，而分子 $\sin x$ 始终在 $[-1,1]$ 之间震荡，从而使得整个表达式趋于 0 的结论。

而饱和数学的思想是一种近似工具——在这种方法里，我们人为地规定了一个「最大值」来代表无穷大，以及一个「最小值」来代表无穷小。例如，若我们规定：

那么当我们考虑极限 $\lim_{x\to+\infty}\frac{\sin x}{x}$ 时，就可以作如下近似换算：

代入无穷大数值：
把 $x$ 取为 65536，此时表达式为 $\frac{\sin(65536)}{65536}.$
对分子估值：
由于 $\sin(65536)$ 依然在 $[-1,1]$ 之间，其绝对值最大也不会超过 1。
计算近似值：
因此，该比值的绝对值不超过 $\frac{1}{65536} \approx 0.00001526$, 这个数值远小于我们规定的「无穷小」界限 0.0001。

在这种约定下，我们便认为当 $x$ 取代「无穷大」（即 65536）时，$\frac{\sin x}{x}$ 的值已经小到可以近似看作无穷小，从而近似等于 0。

总结：
利用饱和数学的思想，把 $+\infty$ 视为 65536，无穷小界限定为 0.0001，那么

$\lim_{x\to+\infty}\frac{\sin x}{x} \approx 0$
,

这与传统意义下的极限结果一致。

注意：
这种方法本质上是一种数值近似和工程上的取舍，虽然在某些情况下能够给出直观的近似结果，但它不能替代严谨的极限理论。实际数学证明中，我们仍然需要依赖极限的定义和分析方法进行严密证明。

在饱和数学的思想中，我们人为地将「无穷大」与「无穷小」固定为具体数值（例如：无穷大取 65536，无穷小界定为 0.0001），从而用数值近似的方法对极限进行计算。对绝大多数传统收敛的极限问题，这种做法通常能给出符合直觉的近似结果；例如：

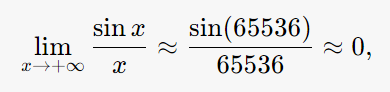
因为即便 $\sin(65536)$ 在 $[-1,1]$ 之间震荡，其结果与 65536 相比，绝对值都很小（远低于 0.0001）。

对于一个不收敛的极限，取不同的代表性数值代入（例如用 0.0001、0.0002、0.0003 来近似代表「趋近于 0」或其他趋近过程）往往会得到不稳定或剧烈变化的结果。原因如下：

数值代入的代表性
饱和数学采用固定数值来代表极限过程中的「无穷小」或「无穷大」。当一个函数的极限不存在时，它的数值行为不会在某个固定点附近趋向唯一值，而是表现出剧烈波动或者依赖于代入点的选取。例如，考虑函数

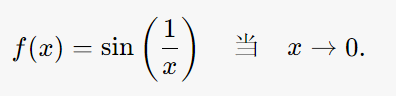
按传统极限理论，此时 $x\to 0$ 并没有收敛到一个确定的值，因为 $\frac{1}{x}$ 会趋向无穷大，从而 $\sin\left(\frac{1}{x}\right)$ 在 $[-1,1]$ 内不断震荡。

依次代入不稳定数值
如果用饱和数学的方法，假设我们定义 0.0001 为一个代表性的「无穷小」值，那么
- 当 $x=0.0001$ 时，$f(0.0001)=\sin(10000)$；
- 当 $x=0.0002$ 时，$f(0.0002)=\sin(5000)$；
- 当 $x=0.0003$ 时，$f(0.0003)=\sin(3333.\overline{3})$；
这三个值由于参数分母的变化，会导致 $\sin$ 函数的输入值在很大范围内变化，从而得到剧烈不同的输出。如果我们按饱和数学的思路来看，每个替代的「无穷小」值都会给出不同的结果，从而说明该极限根本不稳定或不收敛。
数值稳定性与极限收敛性的关系
- 收敛的极限：当我们用不同的代表数值（如 65536 或 0.0001）进行代入后，结果基本保持稳定（与理论极限一致）。
- 不收敛的极限：不同的代表值会导致截然不同的结果，反映出函数在该趋近过程中不存在唯一的极限值。这种不稳定性正是「不收敛」的数值体现。

收敛情况：饱和数学通过将无限过程中的极大或极小量替换为具体数值，可以给出与传统极限理论一致且稳定的近似结果。
不收敛情况：如果极限不收敛（例如函数在趋近过程中震荡或无界），通过依次代入不同代表性值（如 0.0001、0.0002、0.0003）通常会得到变化剧烈的不稳定结果，这正反映了该极限缺乏收敛性的本质。

这种方法虽然在工程和某些近似计算中可能有直观上的帮助，但它不具备严格的数学证明效力。在严格数学分析中，我们依然需要借助极限定义等严谨工具来讨论函数收敛与否。