想象一下,你正站在一个热闹的派对上,四周是成千上万的客人,每个人都在低声交谈,却没有人单独主导整个对话。突然,一个有趣的话题出现——不是某一个人大声宣布,而是大家集体微微转向,声音交织成一股清晰的浪潮,让你瞬间明白他们在聊什么。这就是大脑和人工智能(AI)处理信息的奇妙方式:不是靠某个「明星」神经元或节点独挑大梁,而是通过一群单元的集体舞蹈,来描绘出复杂的概念和刺激。神经科学中的群体编码理论,与AI中的分布式表征,正是这场派对的完美隐喻,它们共同揭示了高效、鲁棒的信息处理原则,仿佛大自然和工程师不约而同地选择了同一本「秘籍」。
🧠 群体编码的集体智慧:大脑如何用合唱团演绎世界
在神经科学领域,群体编码就像一支训练有素的合唱团:单个神经元可能对多种刺激略有响应,但真正表征一个特定概念——比如一个方向、一张面孔或一个声音——的是整个群体的激活模式。想象一下,在灵长类动物视觉皮层中,一个边缘方向的刺激不会只点亮一个神经元,而是唤醒一群对类似方向敏感的细胞,形成一个平滑的「响应山丘」。这种分布式方式带来的好处显而易见:如果某个歌手(神经元)感冒了,合唱团的声音依然动听——这就是鲁棒性,对噪声和损伤的强大容忍。
更妙的是,这种编码允许大脑高效存储海量信息。单个神经元对多刺激响应,群体组合起来就能指数级扩展表示容量,正如参考文献中灵长类面部识别实验所示,特定面孔激活整个区域的多个神经元群。比起「一对一」的局部编码,这就像用一幅印象派画作而不是单色块来描绘风景:细节丰富,容错更高。
为了更直观地比较群体编码与AI分布式表征的关键属性,这里是一个表格:
| 方面 | 神经科学中的群体编码 | AI中的分布式表征 |
|---|---|---|
| 基本单元 | 单个神经元对多刺激响应 | 单个隐藏节点捕捉多特征 |
| 表示机制 | 刺激激活神经元群体,形成激活模式 | 概念由高维向量编码,非局部化 |
| 优势 | 鲁棒(噪声容忍)、高效(容量大) | 泛化强、容错高 |
| 示例应用 | 方向选择性、面部识别 | 词嵌入、图像分类 |
| 数学描述 | 响应曲线、贝叶斯解码 | 嵌入空间、余弦相似度 |
这个表格清晰地展现了二者的结构性对齐,仿佛进化与梯度下降算法在同一个几何空间中相遇。
注解:群体编码的概念可能对非专业读者有些抽象。它本质上是「大脑不把信息锁在单个细胞里,而是分散到一群细胞的集体活动中」。这类似于日常生活中的团队决策:一个人可能出错,但团队共识更可靠。参考实验显示,这种方式让大脑在复杂环境中(如噪声干扰)仍能准确解码刺激,至少提升了数倍的信息容量。
基于此,我们进一步探索几何视角:大脑的神经活动并非乱糟糟的高维散点,而是优雅地约束在一个低维「流形」上。
🌌 神经流形的优雅几何:从高维混乱到低维秩序的魔法
试想一下,你在高维空间扔出一把沙子——维度等于神经元数量,可能成千上万。但神奇的是,这些沙粒不会随意飞散,而是落在一条光滑的曲线上,或一个环状的表面上。这就是神经流形理论的核心:神经元群体的活动嵌入低维几何结构中,形成任务相关的内部空间。
比如,在小鼠海马体中,空间导航的活动形成环形流形,像一个隐形的圆环编码位置信息;在视觉系统中,它可能是连续曲面,支持从纠缠输入到清晰表征的「解缠」。这种低维约束减少了计算负担,却保留了关键变异——就像把一张皱巴巴的地图展平,却不丢失任何道路细节。
在AI模型中,这种现象自发涌现:训练过程中,激活空间从随机噪声演变为低维流形。工具如主成分分析(PCA)或持久同调揭示,生物与人工系统的拓扑相似——点云更接近环面而非球面。架构影响几何:前馈网络(如CNN)倾向不连续流形,类似视网膜孤立电路;循环网络(如RNN)生成连续流形,镜像初级视觉皮层的重叠连接。
以下表格概述神经流形在生物与人工网络的比较:
| 属性 | 生物神经网络 | 人工神经网络 |
|---|---|---|
| 维度降低 | 高维活动嵌入低维流形 | 激活空间自发形成低维子空间 |
| 几何特征 | 连续/不连续,环状或曲面拓扑 | 类似拓扑,如点云接近环面 |
| 影响因素 | 电路连接性(如孤立 vs. 重叠) | 架构(前馈 vs. 循环) |
| 功能作用 | 表征解缠、动态认知 | 泛化、抽象化 |
| 分析工具 | PCA、持久同调 | 相同工具,加上稀疏自编码器 |

(图片描述:高维神经空间中的低维环形流形,展示活动轨迹如何约束在优雅几何上。)
注解:流形概念源于数学拓扑,简单说就是「高维数据实际生活在低维曲面中」。这帮助大脑节省能量:不用激活所有神经元,只在流形上「滑动」。在AI中,它解释了为什么模型能从有限训练数据泛化到新刺激——几何约束捕捉了本质变异。
这种几何统一了多模态分析,桥接结构与功能。接下来,我们看到AI中惊人的「脑-like」证据。
🤖 AI中的脑叶奇迹:稀疏自编码器揭开模块化秘密
近年来,大型语言模型(LLM)的内部剖析带来震撼发现:使用稀疏自编码器,研究者看到抽象概念如数学和代码的特征空间形成模块化「lobes」,宛如大脑功能区!
想象LLM的激活空间如一个宇宙:微观层面有「晶体」结构,如平行四边形类比(man:woman::king:queen);中观层面,数学/代码特征聚集成「脑叶」,空间局部性高于随机;宏观层面,非各向同性分布,中间层幂律特征值表明集中表征。
MIT研究显示,LLM中间层形成「语义枢纽」:共享表征空间锚定主导语言(如英语),允许跨模态推理——中文或代码「翻译」成英语-like标记。干预实验证实,修改英语状态影响其他模态,镜像人类前颞叶整合多感官。
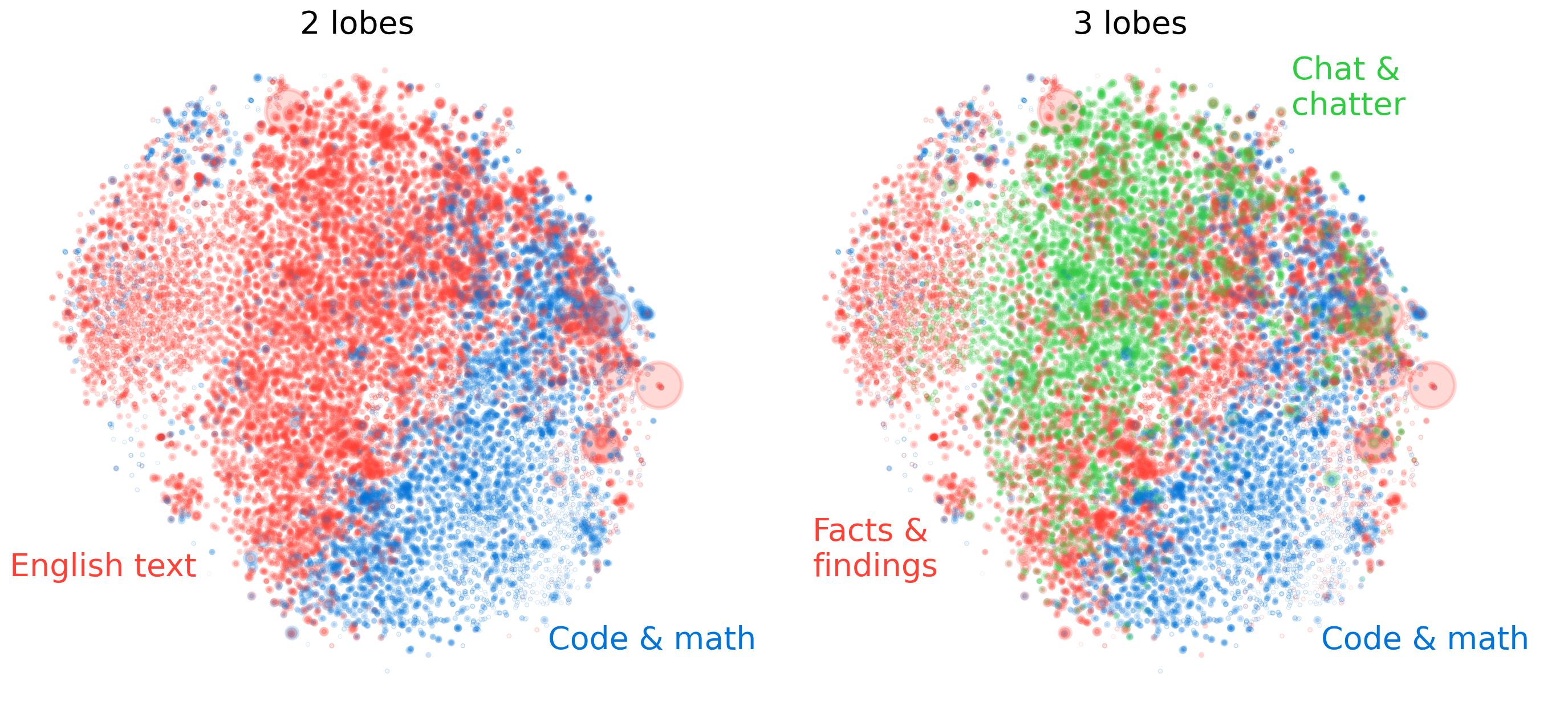
(图片描述:特征点云中,功能相似组形成几何「lobes」,类似fMRI大脑功能区。)
这些涌现自训练优化,非特定实现,暗示普适数学原则。基于此,群体编码与分布式表征的契合扩展到几何层面。
🌉 普适原则的曙光:从生物进化到AI优化的共通框架
回溯开头派对隐喻:大脑与AI的集体编码并非巧合,而是优化信息处理的必然结果。高维空间中的分布式模式,提供鲁棒、高效、泛化——进化青睐它,梯度下降重现它。
神经流形作为内部表征空间,支持动态解缠和抽象化;LLM中的「脑叶」和语义枢纽,镜像认知过程。尽管细节因脑区或模型而异,证据日益强劲:这些模式源于数学普适性,推动神经科学与AI融合。
想象一下,你正目睹一场跨界对话:神经元群体低语着方向与面孔,AI向量吟诵着代码与数学。它们共享几何语言,揭示高效智能的本质。这不仅深化对大脑的理解,还为设计更鲁棒AI铺路——或许,下一个突破,就藏在这些低维流形的优雅曲线中。
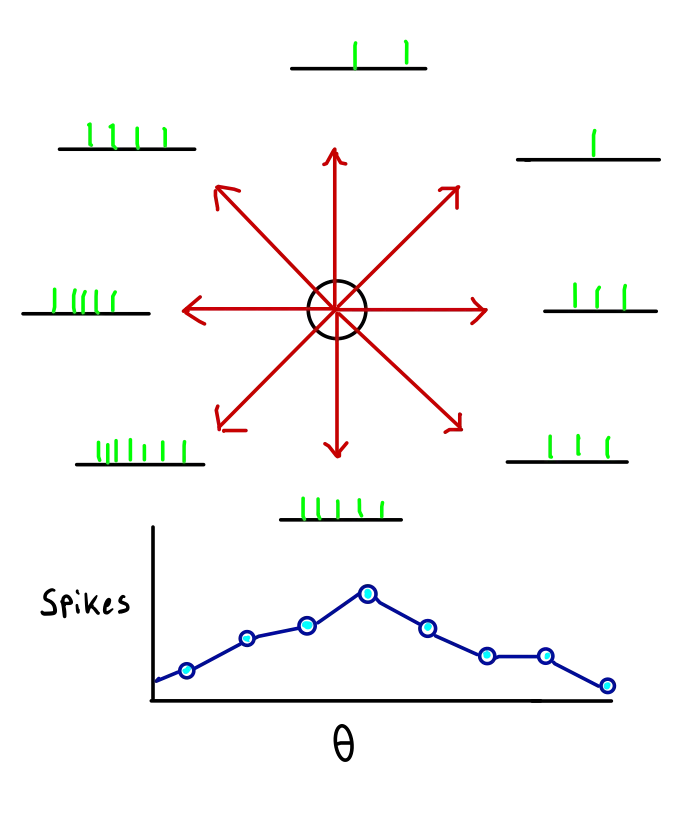
(图片描述:多个神经元调谐曲线,激活向量加权平均编码精确方向。)

(图片描述:词向量空间,语义相近概念聚类,形成分布式模式。)
这种共通框架,让我们看到:智能并非孤岛,而是几何与集体的交响。
参考文献
- Chung, S. , et al. (2021). Neural population geometry: An approach for understanding biological and artificial neural networks. ✅Current Opinion in Neurobiology.
- Liu, Z. (2022). Manifold Structure of Artificial and Biological Neural Networks. Princeton University Honors Thesis.✅
- Michaud, E. J., et al. (2025). The Geometry of Concepts: Sparse Autoencoder Feature Structure. ✅Entropy.
- Wu, Z. , et al. (2025). Like human brains, large language models reason about diverse data in a general way. MIT News.✅
- Vyas, S. , et al. (相关扩展). Neural manifolds and population coding in cognition and AI. Extended from key citations.✅