时间序列分析(Time Series Analysis)详解

1. 时间序列分析的定义和用途

数据会随时间变化，能够识别数据可能变化的方式对于对未来数据做出合理预测至关重要。数据整体上是否呈现稳定上升或下降趋势？是否存在定期出现的波动？也许数据中存在与季节或多年商业周期密切相关的可预测波动。

时间序列分析允许检查在特定时间间隔收集或记录的数据点，从而能够识别趋势、模式和季节性变化，这对于在各个行业中做出明智的预测和决策至关重要。它广泛应用于商业、金融、经济学、环境和天气科学、信息科学以及许多其他随时间收集数据的领域。

注意：时间序列分析的核心是通过分析历史数据中的模式和趋势，来预测未来的数据点，从而帮助决策者做出更明智的选择。

2. 时间序列分析的应用领域

时间序列分析用于解决现实世界问题的一些领域包括：

预测和预测：基于当前和历史数据对未来（未知）数据进行预测可能是时间序列分析最重要的用途。企业使用这些方法来推动战略决策并增加未来收入。政策制定者依靠预测来预测可能影响选举和公共服务需求的人口变化。

风险管理：时间序列分析可以帮助量化风险。例如，保险公司可能预测影响房主未来索赔数量和总金额的趋势，这直接影响保险费。

异常检测：如果数据似乎与预测偏差很大，这可能指向数据某些特征的重大变化，或揭示需要更仔细分析的隐藏因素。例如，如果一个家庭的支出模式显著超过预测水平，这可能表明家庭收入突然增加或潜在欺诈。

医疗保健和流行病学：时间序列分析常用于监测患者生命体征，研究癌症在不同人群个体中的进展情况，追踪疾病爆发，以及预测未来对医疗资源的需求，如疫苗或医院额外床位等。

3. 时间序列分析的基本步骤

时间序列分析涉及许多统计和计算技术，以识别模式、做出预测或获得对数据的洞察。时间序列分析的基本步骤紧密遵循数据科学周期，如下所述：

问题识别/定义：你需要知道什么？你想预测未来几年产品的销售情况吗？你对研究太阳黑子随时间变化的模式感兴趣吗？你对股票的投资可能导致盈利还是亏损？

数据收集：一旦你有了问题，现在你需要数据来分析。如果合适的数据集不存在，这一步可能非常耗时。在最好的情况下，其他人已经收集了你可能可以使用的数据。在最坏的情况下，你需要通过调查、实验、观察或其他方式安排数据收集。

数据清洗：现实世界的数据很少以立即可分析的形式出现。大多数情况下，数据必须清洗，包括以某种方式处理缺失数据，并适当格式化数据以便计算机能够理解它。

模型选择：下一步是将数据拟合到模型。实际上，你可能会发现必须创建许多模型和这些模型的变体，然后才能对结果满意。

模型评估：这可能是最重要的一步。如果你创建的模型不够准确，那么它的实用性将受到限制。模型应该包括一些关于你可以对其预测有多自信的指示。此外，当新的观察值可用时，模型的预测应该与它们进行比较，并根据需要进行调整以更好地拟合数据。

4. 时间序列的定义和特点

任何由同一变量的数值测量组成的数据集，如果按照规律的时间间隔收集和组织，都可以被视为时间序列数据。例如，下表显示了S&P 500（股市上500家顶级上市公司的综合指数）过去几年的数据。这里，变量是每年最后一个交易日的S&P指数值（时间点数据）。

年份	年末S&P指数
2013	1848.36
2014	2058.90
2015	2043.94
2016	2238.83
2017	2673.61
2018	2506.85
2019	3230.78
2020	3756.07
2021	4766.18
2022	3839.50
2023	4769.83

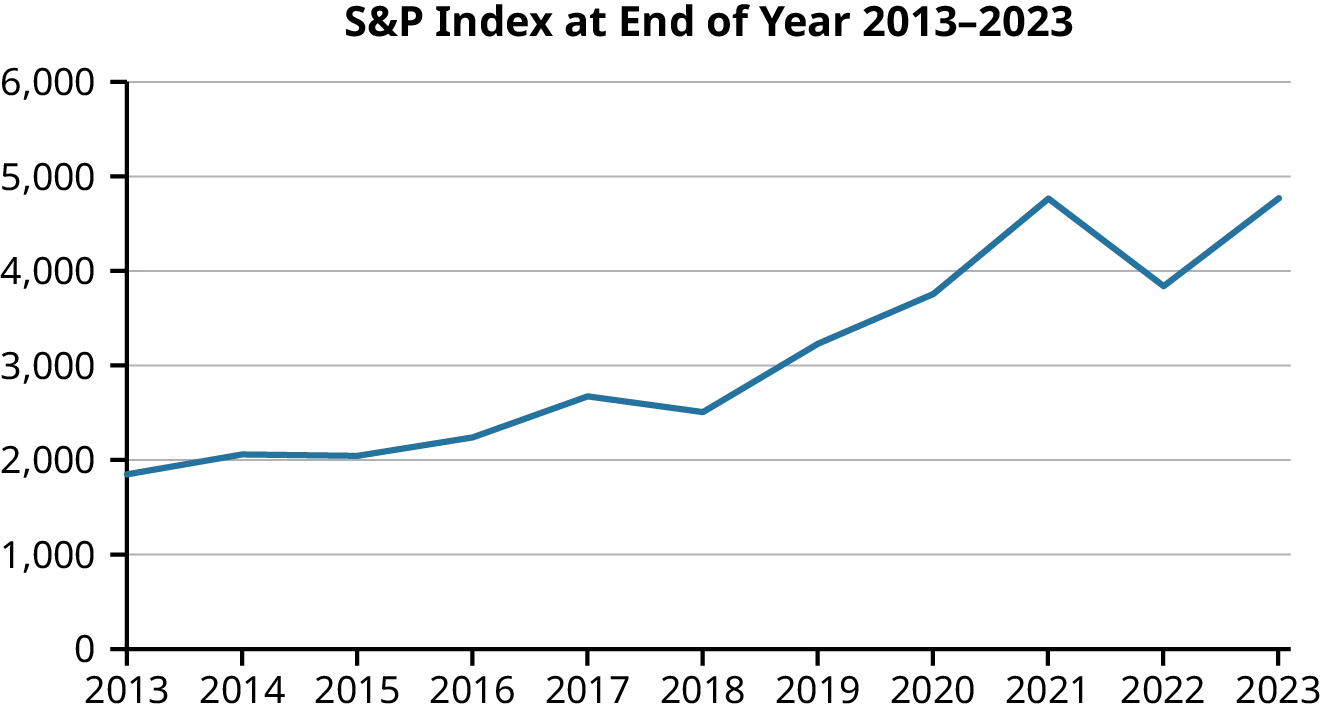
虽然表格信息丰富，但用它来寻找趋势或做出预测并不特别容易。可视化会更好。下图使用时间序列图（本质上是折线图）显示时间序列数据。注意，虽然总体趋势是上升的，但在2018年和2022年也有下降。

2013-2023年末S&P指数

图5.2中显示的示例是一个简单的时间序列，仅跟踪了一个度量（S&P 500指数值）随时间的变化。只要我们记住这些数据代表从2013年开始的S&P 500指数的年度值，将值单独视为有序列表会更有效率。

1848.36, 2058.9, 2043.94, 2238.83, 2673.61, 2506.85, 3230.78, 3756.07, 4766.18, 3839.5, 4769.83

在数学中，数字的有序列表称为序列。序列的各个值称为项。抽象序列可以表示为(x_n)或(x_n)_1≤n≤N。在这两种表示法中，n表示序列每个值的索引，而后一种表示法还指定了序列的索引值范围（n取从1到N的所有索引值）。即：

(x_n)_1≤n≤N = (x₁, x₂, x₃, x₄, …, x_N)

我们将使用标准术语”时间序列”来指代时间标记的数据序列，并在讨论时间序列的项作为值的有序列表时使用术语”序列”。

然而，并非每个数据点序列都是时间序列。世界各国当前人口的集合不是时间序列，因为数据不是在不同时间测量的。但是，如果我们专注于一个国家并逐年跟踪其人口，那么这将是一个时间序列。按年份列出的最受欢迎的婴儿名字怎么样？虽然有时间成分，但数据不是数字化的，因此这不会属于时间序列的范畴。另一方面，关于每年有多少婴儿被命名为”Jennifer”的信息将构成时间序列数据。

通常，我们假设时间序列数据是在相等的时间间隔内采集的，并且没有缺失值。时间序列的项往往以某种方式依赖于先前的项；否则，可能无法对未来项做出任何预测。

5. 时间序列模型的概念

时间序列模型是用于查找、近似或预测给定时间序列值的函数、算法或方法。时间序列模型背后的基本思想是，先前的值应该提供关于未来值如何表现的一些指示。换句话说，存在某种函数，它将时间序列的先前值作为输入，并产生下一个值作为输出：

x_n+1 = f(x_n, x_n-1, x_n-2, …, x₁)

然而，在除了最理想情况之外的所有情况下，能够以完美准确度预测时间序列下一个值的函数并不存在。随机变异和模型中未考虑的其他因素将产生误差，误差被定义为预测与实际观察值之间的差异程度。因此，我们应该始终将误差项（通常用希腊字母ε表示，称为”epsilon”）纳入模型。此外，我们不期望模型精确地产生下一项，而是生成预测值。通常，时间序列的预测值用(x̂_n)表示，以区别于实际值(x_n)。因此：

x̂_n+1 = f(x_n, x_n-1, x_n-2, …, x₁, ε)

6. 时间序列预测的方法

通常，时间序列分析的目标是对时间序列的未来值进行预测或外推，这个过程称为预测。作为一般规则，随着预测进一步推向未来，预测的准确性会降低。当未来的预测不再比抛硬币或掷骰子更准确时，在该点或更远处的预测就变得无效。在实践中，时间序列模型会定期更新以适应新数据。

根据情况和数据的性质，有许多不同的方法来预测未来数据。所有方法中最简单的，称为朴素或平坦预测方法，是使用最近的值作为下一个值的最佳猜测。例如，由于S&P 500在2022年底的价值为3,839.5，可以合理地假设在2023年底的价值将相对接近3,839.5。注意，这将对应于时间序列模型x̂_n+1 = x_n。朴素方法在实践中只有有限的用途。

不是仅使用最后一个观察值来预测下一个值，更好的方法可能是考虑多个值x_n, x_n-1, x_n-2, …，来找到估计值x̂_n+1。人们可以将最后的T个值平均在一起（对于某些预定义的T值）。这被称为简单移动平均，将在时间序列分析的组成部分中明确定义。现在，让我们直观地说明这个想法。假设我们使用最近的T=3个项的平均值来估计下一项。时间序列模型将是：

x̂_n+1 = (x_n + x_n-1 + x_n-2) / 3

基于表5.1中的数据，2023年底S&P指数值的预测将计算如下：

(4,769.83 + 3,839.5 + 4,766.18) / 3 = 4,458.5

预测的另一种简单方法是将数据拟合到线性回归模型，然后使用回归模型预测未来值。与仅使用最后一个数据点相比，线性回归在捕捉数据的总体方向方面做得更好。另一方面，线性回归将无法模拟数据中更细微的结构，如周期性模式。此外，还有一个隐藏的假设，即数据在我们希望预测的整个时期内或多或少地均匀上升或下降，这通常不是一个有效的假设。

7. 示例分析：使用线性回归模型预测S&P指数

问题

为表5.1中的数据找到一个线性回归模型，并使用它预测2024年底和2025年底的S&P值。

解决方案

为了解决这个问题，我们可以使用Python中的线性回归模型来拟合数据并进行预测。

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# 准备数据
years = np.array([2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023]).reshape(-1, 1)
sp_values = np.array([1848.36, 2058.90, 2043.94, 2238.83, 2673.61, 2506.85, 3230.78, 3756.07, 4766.18, 3839.50, 4769.83])

# 创建并拟合线性回归模型
model = LinearRegression()
model.fit(years, sp_values)

# 预测2024年和2025年的值
future_years = np.array([2024, 2025]).reshape(-1, 1)
predictions = model.predict(future_years)

# 输出预测结果
print(f”2024年预测S&P指数值: {predictions[0]:.2f}”)
print(f”2025年预测S&P指数值: {predictions[1]:.2f}”)

# 可视化结果
plt.figure(figsize=(10, 6))
plt.scatter(years, sp_values, color=‘blue’, label=‘实际值’)
plt.plot(years, model.predict(years), color=‘red’, label=‘回归线’)
plt.scatter(future_years, predictions, color=‘green’, label=‘预测值’)
plt.xlabel(‘年份’)
plt.ylabel(‘S&P指数值’)
plt.title(‘S&P指数线性回归预测’)
plt.legend()
plt.grid(True)
plt.show()

在这个例子中，我们使用了线性回归模型来拟合S&P指数的历史数据，并预测了2024年和2025年的值。线性回归模型可以帮助我们捕捉数据的总体趋势，但它可能无法捕捉数据中的周期性波动或其他复杂模式。

注意：在本章中，我们将开发更复杂的工具，可以检测平均值或线性模型无法找到的模式，包括自回归模型、移动平均和自回归综合移动平均(ARIMA)模型。然而，为时间序列数据创建花哨的模型只是过程的一部分。过程的一个重要部分是测试和评估你的模型。因此，我们还将探索误差和不确定性的度量，这些可以确定模型有多好以及其预测可能有多准确。