Pre-Norm与Post-Norm:深度学习归一化架构的演进与选择
深入理解大模型架构设计中的关键技术
architecture 定义与基本原理
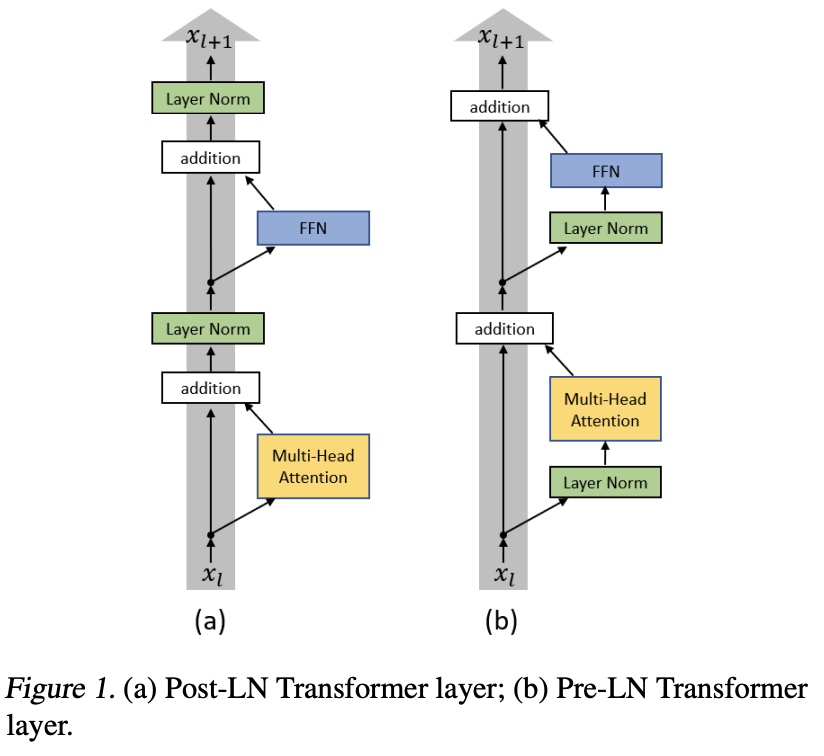
Post-Norm
xt+1 = Norm(xt + F(xt))
传统Layer Norm放在残差之后,做完Add再进行归一化。早期模型如BERT采用此架构。
Pre-Norm
xt+1 = xt + F(Norm(xt))
先对输入做Layer Norm,然后再进行函数计算以及Add相加。现代大模型如GPT、LLaMA采用此架构。
compare_arrows 梯度传播与训练稳定性差异
| 特性 | Post-Norm | Pre-Norm |
|---|---|---|
| 梯度分布 | 靠前层梯度小,靠后层梯度大 | 靠前层梯度大,靠后层梯度小 |
| 梯度稳定性 | 不稳定,容易梯度爆炸 | 稳定,各层梯度量级均衡 |
| 训练收敛 | 困难,需要warmup机制 | 快速,收敛性好 |
| 网络深度 | 保持真实网络深度 | 深度虚化,等效于更宽的网络 |
error_outline Post-Norm的问题和局限性
cancel主要问题
- 梯度消失:浅层信号贡献度以1/2l/2指数衰减
- 训练不稳定:梯度容易爆炸,学习率敏感
- 初始化权重敏感:需要精细调参
- 收敛困难:必须使用warmup机制
- 残差路径失效:LayerNorm成为梯度衰减的放大器
check_circle理论优势
- 特征一致性:每层输出严格归一化
- 微调友好性:梯度衰减抑制浅层参数更新
- 理论性能上限:保持真实网络深度
- 中间层特征抽取:可直接用于下游任务
trending_up 为什么大模型现在都使用Pre-Norm架构
check_circlePre-Norm优势
- 训练稳定性:残差路径无缩放干扰
- 收敛性好:不需要warmup机制
- 即插即用:降低调参难度
- 支持千层级网络训练
- 适合大规模模型:训练成本效益高
cancelPre-Norm局限
- 深度虚化:层数越多,层数越」虚」
- 理论性能上限较低:同等参数量下表征能力弱
- 需要增大FFN层维度补偿深度损失
- 中间层特征抽取需额外归一化处理
工程实践选择:小模型/需特征抽取优先Post-Norm(如BERT),大模型/训练效率优先必选Pre-Norm(如GPT、LLaMA)
new_releases 新的Norm架构:RMSNorm
RMSNorm(均方根归一化)
RMSNorm(x) = γ ⊙ x / RMS(x)
其中:RMS(x) = √(1/d ∑xi∈x xi2 + ε)
| 特性 | LayerNorm | RMSNorm |
|---|---|---|
| 计算均值 | 是 | 否 |
| 计算复杂度 | 较高 | 较低 |
| 计算速度 | 1× | 1.6× |
| 内存占用 | 1× | 0.8× |
| 适用场景 | NLP、Transformer | 大规模语言模型、低精度计算 |
应用:已被广泛应用于LLaMA、Gemma等大规模语言模型,主要用于提升推理速度、减少计算开销,并适应低精度计算(FP16、BF16)。
