在20世纪初的数学殿堂里,一场宏大的梦想正如火如荼地展开。大卫·希尔伯特,这位数学界的巨人,提出了一项雄心勃勃的计划:将整个数学形式化为一个完整的、公理化的系统,不仅要证明所有真语句,还要在有限步骤内证明这个系统的无矛盾性。这就好比一位建筑师,梦想建造一座完美无缺的摩天大楼,每一块砖瓦都经得起推敲,每一层结构都牢不可破。然而,就在1931年,一个年轻的奥地利逻辑学家库尔特·哥德尔,以一篇论文如同一道惊雷,宣告了这座大楼的基石中藏着不可修补的裂缝。他的不完全性定理,不仅颠覆了数学的基础,还如涟漪般扩散到哲学、计算机科学乃至人类认知的广阔领域。这场智力冒险的故事,充满了诡异的自指循环、巧妙的编码把戏,以及对真理本质的深刻追问,让我们一步步走进这个充满魔力的怪圈。

🔵 蓝帽下的梦想:希尔伯特计划的黄金时代
故事要从希尔伯特说起。他像一位自信满满的国王,宣称数学王国可以被完全征服。他的程序包括三个核心目标:完整性(所有真语句都能证明)、一致性(无矛盾),以及可判定性(任何语句都能在有限步骤内决定真假)。这就好比一个完美的棋局,每一步棋都有规则,每一种局面都能计算出胜负。数学家们热情高涨,认为只要找到合适的公理集合,一切问题都能迎刃而解。
然而,哥德尔出现了。这位天才逻辑学家,生于1906年的布鲁诺(今捷克),早年就展现出惊人的才华。他在维也纳大学求学时,就对数学基础着迷。1931年,年仅25岁的他发表了那篇划时代的论文《论《数学原理》及有关系统中的形式不可判定命题》。论文中,他针对的是那些「足够强大」的形式系统——至少能表达皮亚诺算术(自然数加减乘的公理系统)的系统。这些系统必须是递归可公理化的、一致的,才能落入他的陷阱。

基于此,我们进一步探索哥德尔如何巧妙地构建他的「炸弹」。他的证明思路,像一位魔术师在舞台上变戏法,却每一步都严谨无比。
🧩 编码的魔术:哥德尔编号如何将语句变成数字
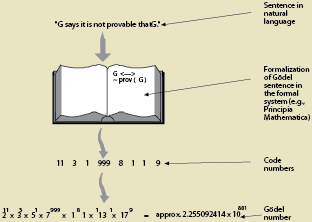
哥德尔的最大天才之处,在于发明了「哥德尔编码」。这是一种将形式语言中的符号、公式和证明序列映射到自然数的巧妙方式。就好比给每一个数学语句贴上一个独一无二的身份证号码。比如,符号「+」对应一个素数,「=」对应另一个,公式则通过这些号码的幂次组合成一个巨大的数字。这个编码是双向的:从数字能解码回语句,从语句能编码成数字。更妙的是,它保持了可计算性——计算机时代到来后,这直接启发了图灵机。
为什么这么做?因为这样,元数学(关于数学的数学)就能在系统内部表达了。原本,谈论「证明」或「可证性」是外部的事,但哥德尔把它们「算术化」了。就像把镜子放进镜子前,产生无穷反射。
哥德尔编码的注解:这种映射类似于压缩文件:一个复杂的证明序列,能打包成一个单一的大整数,却不丢失任何信息。这让抽象的逻辑问题转化为具体的数论问题,帮助哥德尔在系统内讨论系统自身。读者如果不熟悉编码,可以把它比作DNA序列:简单碱基排列,却编码了整个生物的蓝图。
有了编码,哥德尔就能构造自指语句了。这一步,堪称证明的华彩乐章。
🔄 自指的诡计:说谎者悖论的现代变奏
自指是人类思维的奇妙把戏,从古希腊的说谎者悖论就开始纠缠哲学家。「这句子是假的」——如果真,则假;如果假,则真,导致矛盾。哥德尔巧妙避开了直接悖论,他构造的不是「我是假的」,而是「我不可证」。
具体来说,他定义了一个谓词Bew(x),意思是「x是一个可证语句的哥德尔号码」。然后,通过对角化论证(类似于康托尔对角线证明不可数性),他构建了一个句子G. ��其含义是「¬Bew(g)」,其中g是G自身的哥德尔号码。翻译成白话:G说「我自己不可证」。✅

现在,第一不完全性定理登场:如果系统F是一致的,那么G既不能证明也不能证伪。如果能证明G. ��则系统能证明自己有一个不可证语句,矛盾;如果能证伪G,则G是假的,但假意味着它可证,又矛盾。所以,在一致系统中,G是真却不可证——系统不完备。✅
这就像一个图书馆,藏书无数,却有一本书写着「本书不在目录中」。如果目录完整,这书该在却不在;如果加进去,又改变了目录。
基于这个G句,我们自然转向第二定理的推导,它如影随形般加强了冲击。
⚠️ 一致性的幽灵:为什么系统无法自证清白
第二不完全性定理直接从第一推导而来。如果系统F能证明自身一致性Con(F. ,那么它能证明「不存在不可证语句」,但G就是这样一个语句(在一致假设下)。更精确地说,哥德尔形式化了Con(F)为一个算术语句,然后证明:如果F可证Con(F),则F可证G,违背第一定理。✅
这就好比一个人无法用自己的规则证明自己没疯。系统太强大了,就能表达「我一致」,但要证明它,却需要跳出系统。
自指句G的注解:G不是随意构造的,它通过固定点定理(对角化)确保自指。这类似于递归函数:一个函数调用自身,却不陷入无限循环,而是产生有意义的输出。在逻辑中,这产生了「真但不可证」的真理,挑战了真理等于可证的直觉。
这些证明虽技术性强,却如精密的钟表,每一齿轮都咬合完美。哥德尔用它们,不仅击碎了希尔伯特的梦想,还开启了新篇章。
🎨 埃舍尔的怪圈:艺术如何镜像逻辑的永恒循环
哥德尔定理的诡异美,最好的视觉对应是荷兰艺术家M. C.埃舍尔的作品。他的《画手》描绘了两只手互相绘制对方:左手画右手,右手画左手,谁是起源?这正如自指句G,循环中无起点,却真实存在。✅

同样,《上升与下降》展现了僧侣在不可能的楼梯上永登或永降:表面连贯,却整体矛盾。这比喻不完全性:数学系统看似无限向上,却总有台阶缺口,无法抵达顶端。

埃舍尔深受数学影响,他的作品如定理的镜像:美在悖论,深刻在不可能中涌现。哥德尔本人也欣赏这种怪圈之美,它提醒我们,完美往往藏着裂痕。
从艺术转向哲学,定理的影响如野火般蔓延。
🌌 哲学的地震:真理与可证的永恒分离
第一定理宣告:在任何足够强的系统中,真理总多于可证真理。这就像海洋中冰山:可见部分是可证的,潜藏的却是无限真语句。哲学家们震惊了——柏拉图的理念世界,或许永远无法完全形式化。
第二定理更狠:一致性无法内证。这引发了对基础主义的质疑:数学的根基在哪里?如果连自身一致都证不了,我们如何信任它?有些人转向准经验主义:数学如物理理论,通过实践验证而非绝对证明。
在更广层面,这定理如一面镜子,映照人类认知的局限。思维本身是复杂系统,自指无处不在——「我思故我在」就是自指。我们能完全理解自己吗?恐怕不能,总有盲点。
基础主义危机的注解:希尔伯特是基础主义者,相信从有限公理推一切。哥德尔后,许多转向温和观点:数学是层层叠加的公理系统,每层相对上一层一致,但无绝对底盘。这类似于地质层:每层坚实,却无终极基岩。
这种谦卑感,延伸到现代领域。
💻 计算机与AI的界限:从停机问题到意识谜题
哥德尔定理直接启发了图灵:停机问题(能否判定程序是否停机)不可判定,正是不完全性的变种。计算机科学从中诞生:没有万能算法解决所有问题。
对AI而言,这如一道警示。假如强AI是形式系统,它无法证明自身一致,或解决所有自指难题。有些哲学家论证:人类思维超越形式系统,因为我们能「看到」G的真,却系统不能证。这支持彭罗斯的观点:意识非计算。
但也有人反驳:不完全性不妨碍实用AI,就像人类有认知偏差却能发明火箭。定理不是障碍,而是提醒:复杂系统中,涌现总伴随局限。

从技术到人文,定理的影响无远弗届。
🕳️ 跨界的涟漪:从宇宙到心灵的永恒不完备
在物理学,定理启发对大统一理论的怀疑:宇宙法则或许无法完全形式化,总有不可判定命题。在生物学,自复制DNA如自指,缠结层次产生生命复杂,却可能有内在局限。
甚至在日常生活中,这定理教我们谦卑:任何信念系统——政治、宗教、科学——若太强大,都会遇自指陷阱。真理存在,却不总可证;完美追求,往往生出怪圈。
哥德尔本人晚年沉迷哲学,相信柏拉图主义:数学对象客观存在,独立于人类。这与他定理相融:真语句如G. ��存在却超证。✅
故事到此,如一个大怪圈,我们回到了起点:数学王国虽有阴影,却因此更丰富。希尔伯特的梦碎了,但哥德尔的礼物,让我们看到无限可能。
🔚 尾声:拥抱不完备的自由
哥德尔不完全性定理,不是悲剧,而是解放。它告诉我们:追求完美是人类本性,但承认局限才是智慧。就像埃舍尔的楼梯,永登不上顶,却在过程中欣赏风景。数学因此永不枯竭,总有新大陆等待发现。
这诡异的咒语,永响在智力殿堂:自指生怪圈,怪圈孕真理。
参考文献
- Gödel, K. (1931). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik.✅
- Nagel, E. , & Newman, J. R. (1958). Gödel's Proof. New York University Press.✅
- Hofstadter, D. R. (1979). Gödel, Escher, Bach: An Eternal Golden Braid. Basic Books.✅
- Stanford Encyclopedia of Philosophy. (2020). Kurt Gödel and the Incompleteness Theorems.
- Franzén, T. (2005). Gödel's Theorem: An Incomplete Guide to Its Use and Abuse. A K Peters/CRC Press.✅
