🌌 引子：哲学的乌鸦飞过头顶
在一个宁静的午后，你坐在公园的长椅上，手里拿着一本书，偶然抬头，看到一只乌鸦从远处飞过。它的羽毛漆黑如墨，阳光下泛着微光。你心里一闪而过一个念头：「所有乌鸦都是黑色的。」这似乎是一个再平常不过的观察，但哲学家和逻辑学家却不这么认为。
现在，假设你低头看见脚边有一个绿色的苹果。问题来了：这个绿色的苹果，居然也能支持「所有乌鸦都是黑色的」这一假设！这听起来是不是有点荒谬？欢迎来到博伊尔-拉普拉斯的乌鸦悖论，一个挑战直觉、颠覆逻辑的经典哲学问题。
🧠 悖论的核心：乌鸦与苹果的奇妙关联
悖论的提出
乌鸦悖论最早由博伊尔和拉普拉斯提出，其核心围绕一个简单的逻辑假设展开：
假设：所有乌鸦都是黑色的。
在逻辑学中，这一命题可以被等价转换为：
所有非黑色的事物都不是乌鸦。
这两句话在逻辑上是完全等价的，但它们的表述方式却带来了令人费解的悖论。按照逻辑等价性，如果你观察到一个绿色的苹果（它是非黑色的，并且不是乌鸦），这实际上支持了「所有非黑色的事物都不是乌鸦」。由于这与原假设等价，因此，绿色苹果也支持了「所有乌鸦都是黑色的」。
等等，什么？一个苹果怎么能证明乌鸦的颜色？
🔍 逻辑的羽翼：从乌鸦到苹果的推理
逻辑等价的魔法
为了更好地理解这个悖论，我们需要拆解逻辑等价的概念。假设我们用符号来表示：
- $P(x)$ 表示「$x$ 是乌鸦」
- $Q(x)$ 表示「$x$ 是黑色的」
那么，命题「所有乌鸦都是黑色的」可以写成：
![\[\forall x \, (P(x) \rightarrow Q(x))\]](https://jieyibu.net/wp-content/ql-cache/quicklatex.com-132ad0c121792b4e9ce95943b54a1f25_l3.svg "Rendered by QuickLaTeX.com")
这句话的等价形式是：
![\[\forall x \, (\neg Q(x) \rightarrow \neg P(x))\]](https://jieyibu.net/wp-content/ql-cache/quicklatex.com-5cda7c5d67f91265f023f8ebf312a67d_l3.svg "Rendered by QuickLaTeX.com")
翻译成自然语言就是：「所有非黑色的事物都不是乌鸦。」这意味着，任何一个非黑色且非乌鸦的物体（比如绿色的苹果）都可以被视为对这一命题的支持。
证据的两种形式
在这个逻辑框架下，支持「所有乌鸦都是黑色的」有两种方式：
- 直接证据：观察到一只黑色的乌鸦。
- 间接证据：观察到一个非黑色的非乌鸦（比如绿色的苹果）。
这两种证据在逻辑上是等价的，但在直觉上却截然不同。我们通常认为，只有观察到更多的黑色乌鸦才能证明假设，而绿色苹果似乎与乌鸦的颜色毫无关系。这种直觉与逻辑推理的冲突，正是乌鸦悖论的魅力所在。
🍏 绿色苹果的证据：概率的微妙增量
贝叶斯视角：证据的权重
为了进一步理解绿色苹果如何支持「所有乌鸦都是黑色的」，我们可以借助贝叶斯概率的框架。假设我们有一个假设 $H$：「所有乌鸦都是黑色的」，以及一个观察 $E$：「这是一个绿色的苹果」。贝叶斯定理告诉我们：
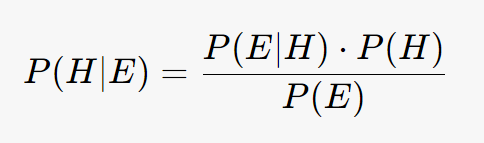
在这里：
- $P(H. $ 是假设 $H$ 的先验概率，即我们在观察之前对该假设的信心。✅
- $P(E|H. $ 是假设为真时观察到 $E$ 的概率。✅
- $P(E. $ 是观察到 $E$ 的总概率。✅
观察到一个绿色苹果（非黑色且非乌鸦）会略微提高 $P(H. $，因为它符合假设 $H$ 的逻辑等价形式「所有非黑色的事物都不是乌鸦」。然而，这种增量非常微小，因为绿色苹果的存在本身对乌鸦的颜色几乎没有直接影响。✅
证据的稀释效应
虽然绿色苹果确实提供了支持，但它的支持力度远不如观察到一只黑色乌鸦。想象一下，如果我们观察到成千上万的非黑色非乌鸦（比如各种颜色的水果），它们对假设的支持会变得越来越稀薄，因为这些观察与乌鸦的颜色关系太过间接。
🦜 语言的陷阱：中文「乌鸦」的黑色偏见
语义与逻辑的冲突
在中文中，「乌鸦」这个词本身就包含了「黑色」的含义。「乌」意为黑色，因此「乌鸦」几乎等同于「黑色的鸦」。如果我们发现了一只非黑色的「乌鸦」，按照中文的语义逻辑，它可能不再被称为「乌鸦」，而是被赋予一个新的名字，比如「黄鸦」或「绿鸦」。
这种语言上的偏见使得乌鸦悖论在中文语境下显得更加复杂。因为在中文中，「非黑色的乌鸦」几乎是一个自相矛盾的概念，它挑战了我们对语言和逻辑的直觉理解。
🌀 悖论的哲学意义：逻辑与直觉的较量
乌鸦悖论不仅仅是一个逻辑游戏，它还揭示了以下深刻的哲学问题：
- 证据确认的复杂性
我们通常认为，只有直接相关的观察才能支持一个假设，但乌鸦悖论提醒我们，间接证据也有其价值。 - 逻辑与直觉的冲突
人类的直觉往往与形式逻辑不一致。我们倾向于忽略绿色苹果对「所有乌鸦都是黑色的」的支持，因为它看起来毫无关联。 - 语言与逻辑的交互作用
语言的使用会影响我们的逻辑推理。在中文中，「乌鸦」的语义暗示了黑色，这种语言偏见可能会阻碍我们对悖论的理解。
🌈 尾声：悖论之外的思考
乌鸦悖论看似荒谬，但它提醒我们，科学和哲学的进步往往来自对直觉的挑战。在日常生活中，我们可能不会因为看到一个绿色苹果就改变对乌鸦颜色的看法，但在科学研究中，每一个看似微不足道的观察都可能为真理的拼图增添一块碎片。
所以，下次当你在公园里看到一只黑色的乌鸦时，不妨想一想：那只乌鸦的颜色，是否真的需要一颗绿色的苹果来证明？
📚 参考文献
- Hempel, C. G. (1945). Studies in the Logic of Confirmation. ✅Mind, 54(213), 1–26.
- Laplace, P. S. (1814). ✅A Philosophical Essay on Probabilities.
- Carnap, R. (1950). ✅Logical Foundations of Probability.
- Goodman, N. (1955). ✅Fact, Fiction, and Forecast.
- Quine, W. V. (1960). ✅Word and Object.