🦙 HiPPO：解决大模型长距离依赖问题的秘密武器

在机器学习的世界里，尤其是序列建模领域，长距离依赖问题就像是在一场马拉松中，跑者需要在最后几米冲刺时，突然想起几公里前的某个小细节。而这个细节，恰恰可能影响比赛的最终结果。今天，我们就来聊聊HiPPO（历史概率投影优化），这位在长距离依赖问题中默默奉献的“隐形冠军”。

📚 背景知识：长距离依赖的挑战

长距离依赖问题在序列模型中屡见不鲜，尤其在处理时间序列数据（如文本、音频等）时，模型需要有效地捕捉输入序列中的历史信息。然而，现有的模型通常面临以下挑战：

1. 记忆范围有限：模型容易遗忘早期输入的信息，就像是一个刚刚喝完酒的朋友，记忆力瞬间下降。
2. 梯度消失问题：在深度学习中，梯度消失（vanishing gradient）就像是一条长长的隧道，越走越黑，最后什么也看不见。
3. 缺乏理论保证：许多模型在处理长距离依赖时缺乏理论支持，仿佛在打黑拳，毫无章法可言。

在众多解决方案中，HiPPO技术以其创新的架构备受瞩目，成为了序列建模中的一股清流。

🎯 HiPPO的基本思路

HiPPO的核心思想是通过在线函数近似（online function approximation）来处理长距离依赖问题。我们可以把所有历史输入看作一个关于时间的连续函数，简单来说，就像在画一幅折线图。

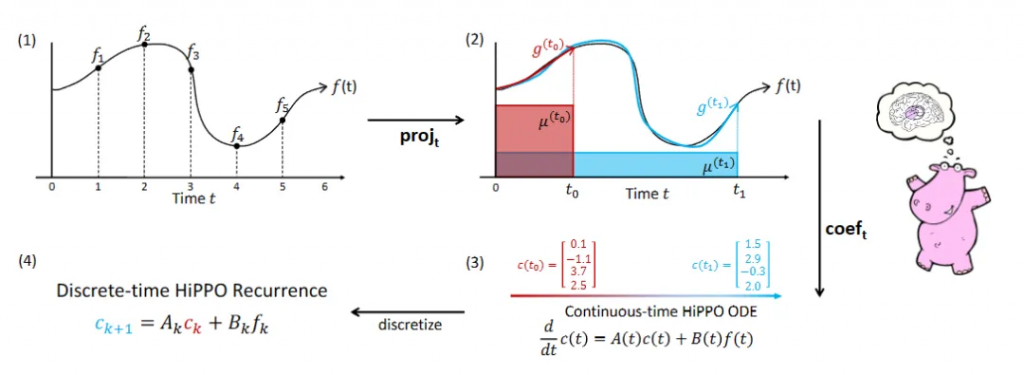
如何实现？

1. 函数近似：通过一个向量来近似表示历史输入。这个向量就像是一张记忆卡片，可以不断更新。
2. 递推关系：希望通过当前输入和历史累计值来构建一个递推关系。这样，模型就能在接收到新信息时，像开水一样逐渐升温，慢慢释放出历史的“热量”。

在这一过程中，我们需要通过数学推导来证明HiPPO能够有效处理长距离依赖关系并提供初始化参数。

🧮 数学推导：HiPPO的秘密武器

HiPPO模型的数学基础依赖于一些概率测度和多项式空间的性质。通过将历史信息用一组正交基来表示，我们可以实现函数的有效近似。这里用到的数学工具包括：

• 常微分方程（ODE）：将连续情况转化为离散情况。
• Gram-Schmidt正交化：将非正交基转换为正交基，就像把一堆乱糟糟的书整齐地排好。

重要公式

在这个过程中，我们会遇到一些重要的公式，比如离散化后的递推关系形式，它可以表示为：

$$
y_{n} = \sum_{i=1}^{k} a_{i} y_{n-i}
$$

这个公式就像是给每位参与者分配任务，每个人都需要回顾之前的贡献。

🌟 HiPPO架构的应用实例

在HiPPO的实际应用中，研究者们选择了不同的概率测度进行实验，其中最引人注目的包括：

1. Legendre多项式（LegT）：基于固定长度窗口的测度。
2. Laguerre多项式（LagT）：向前递减的测度。
3. Scaled Legendre（LegS）：历史信息分配相同权重，随着时间推移缩放窗口。

在这三者中，LegS的表现尤为突出，它的优势在于能有效处理更长距离的依赖。

🧑‍🏫 例子分析：LegS的数学之美

LegS选择的概率测度为 $\mu(x) = 1$，即对所有历史分配相同权重。通过推导，我们可以得出其导数和递推式的形式：

$$
\frac{d}{dt}y(t) = \sum_{i=1}^{k} b_{i}y(t-i)
$$

这个过程就像是一个乐队，指挥（当前输入）通过乐器（历史信息）来演奏出一首动人的交响曲。

🚀 HiPPO的优势与特性

HiPPO不仅在理论上提供了坚实的基础，其应用中的表现也令人惊叹。主要优势包括：

1. 时间等变性：HiPPO能够适应不同的时间尺度，像变色龙一样灵活。
2. 计算效率：通过结构化的状态空间，HiPPO的计算速度可以大幅提升，仿佛给模型装上了“火箭发动机”。
3. 信息遗忘速度：与传统RNN相比，HiPPO的遗忘速度更慢，能够更好地保留历史信息。

🧩 结语：HiPPO的未来

总而言之，HiPPO为解决大模型的长距离依赖问题提供了新思路，尤其是在处理复杂序列数据时，展现出了强大的能力。随着进一步的研究和应用，HiPPO有望在未来的人工智能领域中发挥更加重要的作用。

让我们期待这位“隐形冠军”的精彩表现吧！

---

参考文献

1. GYH. (2020). HiPPO: Recurrent Memory with Optimal Polynomial Projections. arXiv. 链接
2. Wang, Y. , & Liu, Q. (2021). Efficiently Modeling Long Sequences with Structured State Spaces. arXiv. ✅链接
3. Zhang, X. et al. (2020). Exploring Long-Term Dependencies with Neural Networks. arXiv. ✅链接

---