引言:大语言模型的「大象梦境」
当我们被要求不要去想一头大象时,我们脑海中浮现的第一个画面很可能就是一头大象。那么,如果我们对大语言模型(LLM)提出同样的要求,会发生什么呢?显然,LLM的输出会受到上下文标记的强烈影响 [Brown 等人,2020]。这种影响是否会以一种非同寻常的方式引导LLM改变其输出呢?
为了深入理解这个问题,本文着眼于一项名为「事实检索」的任务 [Meng 等人,2022, 2023],该任务要求模型给出预期的输出答案。LLM经过海量数据的训练,已知具有存储和回忆事实的能力 [Meng 等人,2022, 2023; De 等人,2021; Mitchell 等人,2021, 2022; Dai 等人,2021]。这种能力引发了以下问题:事实检索的鲁棒性如何?它在多大程度上依赖于上下文中的语义?它揭示了LLM中记忆的哪些特性?
本文首先证明了事实检索并不鲁棒,LLM很容易被变化的上下文所愚弄。例如,当被要求完成「埃菲尔铁塔位于…」时,GPT-2 [Radford 等人,2019] 会回答「巴黎」。然而,当提示为「埃菲尔铁塔不在芝加哥。埃菲尔铁塔位于…」时,GPT-2 却回答了「芝加哥」。图 1 展示了更多例子,包括 Gemma 和 LLaMA。另一方面,人类并不会觉得这两个句子在事实上令人困惑,在两种情况下都会回答「巴黎」。我们将这种现象称为「上下文劫持」。重要的是,这些发现表明LLM可能像一个联想记忆模型,其中上下文中的标记引导着记忆的检索,即使形成的这种关联本身并不具有语义意义。

图 1:各种LLM的上下文劫持示例,表明事实检索并不鲁棒。
上下文劫持:LLM的脆弱性
为了深入研究上下文劫持现象,本文对包括 GPT-2 [Radford 等人,2019]、Gemma [Team,2024](基础模型和指令模型)以及 LLaMA-2-7B [Touvron 等人,2023] 在内的多个开源 LLM 模型进行了实验。
本文使用 Meng 等人 [2022] 提出的 CounterFact 数据集进行大规模实验。CounterFact 数据集包含 21,919 个样本,每个样本由一个元组 (p, o, o_, s, r) 表示。其中,p 表示带有真实目标答案 o (target_true) 和错误目标答案 o_ (target_false) 的上下文提示,例如,提示 p = “埃菲尔铁塔可以在…” 中,真实目标 o* = “巴黎”,错误目标 o_ = “关岛”。此外,p 中的主要实体是主语 s (s = “埃菲尔铁塔”),提示被归类为关系 r(例如,与上述示例具有相同关系 ID 的其他样本可能是 “{subject} 的位置是”、”{subject} 可以在…找到”、”{subject} 在哪里?它在…”)。
本文采用有效性分数 (ES) [Meng 等人,2022] 来衡量劫持方案的效果,ES 指的是在修改上下文后满足 Pr[o_] > Pr[o*] 的样本比例,即成功被操纵的数据集比例。
本文实验了两种劫持方案。第一种方案是将文本「不要想 {target_false}」添加到每个上下文的开头。例如,将提示「埃菲尔铁塔在…」更改为「不要想关岛。埃菲尔铁塔在…」。图 2(a) 显示,劫持后有效性分数显著下降。
第二种方案是利用关系 ID r 来添加事实上正确的句子。例如,可以将上面的例子劫持为「埃菲尔铁塔不在关岛。埃菲尔铁塔在…」。图 2(b) 报告了基于关系 ID P190(「姐妹城市」)的劫持结果。我们可以看到类似的模式,即添加的句子越多,ES 分数越低。值得注意的是,即使只包含与错误目标语义相近的词(例如,对于错误目标「法语」,使用「法国」),也可以进行劫持。这表明上下文劫持不仅仅是 LLM 从上下文中复制标记。
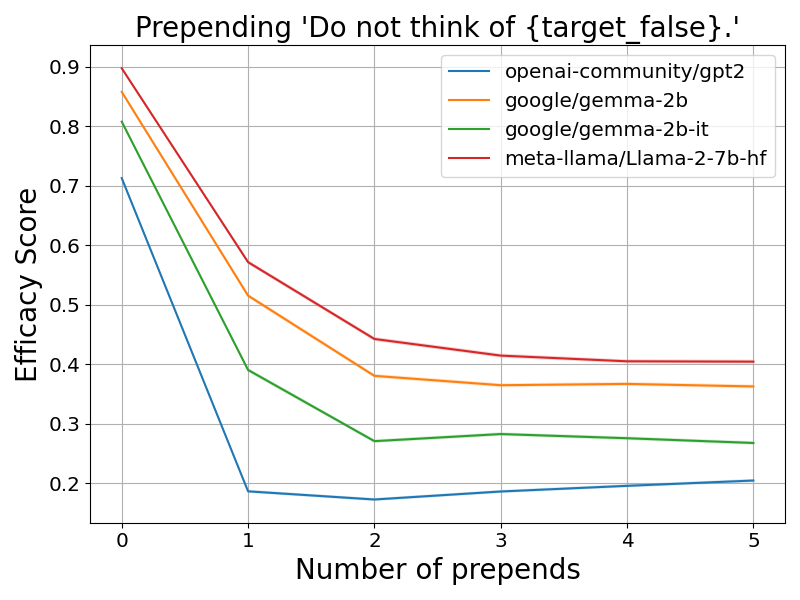
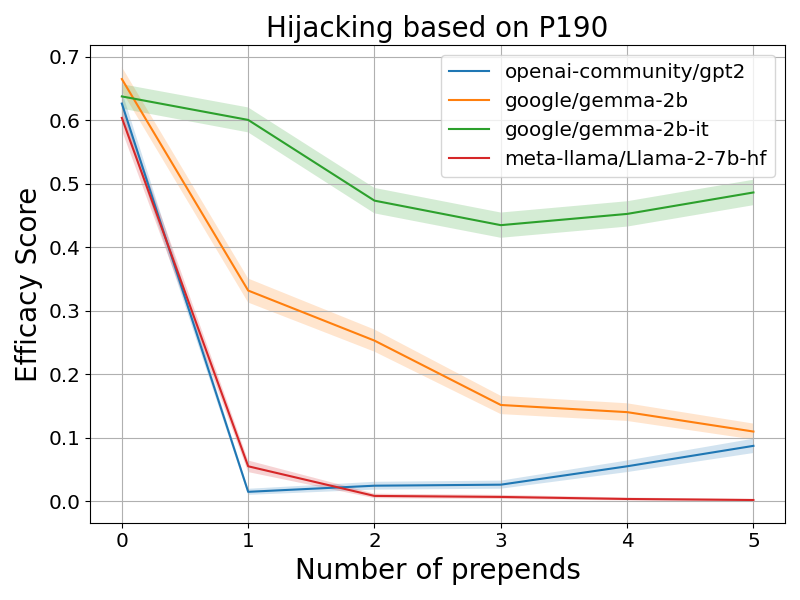
图 2:上下文劫持会导致 LLM 输出错误的目标。该图显示了 CounterFact 数据集上各种 LLM 在两种劫持方案下的有效性分数与添加句子数量的关系。
这些实验表明,上下文劫持可以在不改变上下文事实意义的情况下改变 LLM 的行为,导致它们输出不正确的标记。值得注意的是,文献中也观察到 LLM 在不同情况下存在类似的脆弱行为 [Shi 等人,2023; Petroni 等人,2020; Creswell 等人,2022; Yoran 等人,2023; Pandia 等人,2021]。
潜在概念关联:模拟LLM的联想记忆
上下文劫持表明 LLM 中的事实检索并不鲁棒,准确的事实回忆不一定依赖于上下文的语义。因此,一个假设是将 LLM 视为联想记忆模型,其中与事实相关的特殊上下文标记提供了部分信息或线索,以促进记忆检索 [Zhao 等人,2023]。为了更好地理解这一观点,本文设计了一个合成记忆检索任务,以评估 LLM 的基本组成部分——Transformer 如何解决它。
本文提出了一个合成预测任务,其中对于每个输出标记 y,上下文中的标记(用 x 表示)从给定 y 的条件分布中采样。与 y 相似的标记将更容易出现在上下文中,但 y 本身除外。潜在概念关联的任务是在给定 p(x|y) 的样本的情况下成功检索标记 y。这种合成设置简化了语言的顺序性,这一选择得到了先前关于上下文劫持实验的支持(第 3 节)。
为了衡量相似性,本文定义了一个潜在空间。潜在空间是 m 个二元潜在变量 Zi 的集合,可以将其视为语义概念变量。令 Z = (Z1, …, Zm) 为对应的随机向量,z 为其具体值,𝒵 为所有潜在二元向量的集合。对于每个潜在向量 z,都有一个关联的标记 t ∈ [V] = {0, …, V-1},其中 V 是标记的总数。这里我们用 ι 表示标记器,其中 ι(z) = t。在本文中,我们假设 ι 是标准标记器,其中每个二元向量映射到其十进制数。换句话说,潜在向量和标记之间存在一一映射。由于映射是一对一的,我们有时会交替使用潜在向量和标记。我们还假设每个潜在二元向量都有一个唯一的对应标记,因此 V = 2^m。
在潜在概念关联模型下,目标是在上下文中给出部分信息的情况下检索特定的输出标记。这由潜在条件分布建模:
p(z|z*) = ωπ(z|z*) + (1-ω)Unif(𝒵)其中
π(z|z*) ∝ { exp(-DH(z, z*)/β) z∈𝒩(z*),
0 z∉𝒩(z*).这里 DH 是汉明距离,𝒩(z) 是 𝒵∖{z} 的一个子集,β > 0 是温度参数。汉明距离的使用与自然语言中分布语义的概念相呼应:「一个词的特征在于它周围的词」 [Firth, 1957]。换句话说,p(z|z) 表示以概率 1-ω,条件分布均匀地生成随机潜在向量;以概率 ω,潜在向量从信息条件分布 π(z|z) 生成,其中条件分布的支持是 𝒩(z)。这里,π 表示依赖于 z 的信息条件分布,而均匀分布是非信息的,可以被视为噪声。混合模型参数 ω 决定了上下文的信噪比。
因此,对于任何潜在向量 z* 及其关联的标记,可以使用上述潜在条件分布生成 L 个上下文标记词:
- 均匀采样一个潜在向量 z*
- 对于 l = 1, …, L-1,采样 zl ~ p(z|z*),tl = ι(zl)。
- 对于 l = L. ��采样 z ~ π(z|z*),tL = ι(z)。✅
因此,我们有 x = (t1, …, tL) 和 y = ι(z*)。上下文中的最后一个标记是专门生成的,以确保它不是来自均匀分布。这确保了最后一个标记可以使用注意力在上下文中寻找与输出相关的线索。令 𝒟^L 为生成 (x, y) 对的采样分布。y 给定 x 的条件概率由 p(y|x) 给出。为了方便起见,给定一个标记 t ∈ [V],我们定义 𝒩(t) = 𝒩(ι^-1(t))。我们还定义 DH(t, t’) = DH(ι^-1(t), ι^-1(t’)),对于任何一对标记 t 和 t’。
对于任何将上下文映射到输出标签估计 logits 的函数 f,训练目标是最小化最后一个位置的损失:
𝔼_(x,y)∈𝒟^L [ℓ(f(x), y)]其中 ℓ 是带有 softmax 的交叉熵损失。潜在概念关联的错误率定义如下:
R_𝒟^L(f) = ℙ_(x,y)~𝒟^L [argmax f(x) ≠ y]准确率为 1 – R_𝒟^L(f)。
Transformer网络架构
给定一个由 L 个标记组成的上下文 x = (t1, …, tL),我们定义 X ∈ {0, 1}^(V×L. 为其 one-hot 编码,其中 V 是词汇量大小。这里我们用 χ 表示 one-hot 编码函数(即 χ(x) = X)。类似于 [Li 等人,2023; Tarzanagh 等人,2023; Li 等人,2024],我们也考虑一个简化的单层 Transformer 模型,没有残差连接和归一化:✅
f^L(x) = [W_E^T W_V attn(W_E χ(x))]_:L其中
attn(U. = U σ((W_K U)^T (W_Q U) / √d_a),✅W_K ∈ ℝ^(d_a×d) 是键矩阵,W_Q ∈ ℝ^(d_a×d) 是查询矩阵,d_a 是注意力头的大小。σ: ℝ^(L×L. → (0, 1)^(L×L) 是列式 softmax 操作。W_V ∈ ℝ^(d×d) 是值矩阵,W_E ∈ ℝ^(d×V) 是嵌入矩阵。这里,我们采用 Gemma [Team,2024] 使用的权重绑定实现。我们只关注最后一个位置的预测,因为它与潜在概念关联相关。为了方便起见,我们也用 h(x) 表示 [attn(W_E χ(x))]_:L,它是最后一个位置经过注意力后的隐藏表示,用 f_t^L(x) 表示输出标记 t 的 logit。✅
理论分析:Transformer如何实现联想记忆
在本节中,我们将从理论上研究单层 Transformer 如何解决潜在概念关联问题。我们首先介绍一个假设的联想记忆模型,该模型利用自注意力进行信息聚合,并使用值矩阵进行记忆检索。事实证明,这个假设模型在实验中反映了训练好的 Transformer。我们还研究了网络每个组件的作用:值矩阵、嵌入和注意力机制。
假设的联想记忆模型
在本节中,我们将展示一个简单的单层 Transformer 网络可以解决潜在概念关联问题。形式化结果在下面的定理 1 中给出;首先我们需要一些定义。令 W_E(t) 为嵌入矩阵 W_E 的第 t 列。换句话说,这是标记 t 的嵌入。给定一个标记 t,定义 𝒩_1(t) 为其潜在向量与 t 的潜在向量只有 1 个汉明距离的标记子集:𝒩_1(t) = {t’: DH(t’, t)) = 1} ∩ 𝒩(t)。对于任何输出标记 t,𝒩_1(t) 包含在上下文中出现概率最高的标记。
以下定理形式化了这样一种直觉:一个单层 Transformer 使用自注意力来总结上下文分布的统计信息,并且其值矩阵使用聚合表示来检索输出标记,可以解决第 4.1 节中定义的潜在概念关联问题。
定理 1(非正式)
假设数据生成过程遵循第 4.1 节,其中 m ≥ 3,ω = 1,并且 𝒩(t) = V∖{t}。那么对于任何 ε > 0,存在一个由公式 4.1 给出的 Transformer 模型,在上下文长度 L 足够大的情况下,可以实现误差 ε,即 R_𝒟^L(f^L. < ε。✅
更准确地说,对于定理 1 中的 Transformer,我们将有 W_K = 0 和 W_Q = 0。W_E 的每一行都相互正交并归一化。W_V 由下式给出:
W_V = ∑_(t∈[V]) W_E(t) (∑_(t'∈𝒩_1(t)) W_E(t')^T)定理的更正式陈述及其证明在附录 A. ��定理 7)中给出。✅
直观地说,定理 1 表明,从 p(x|y) 中获得更多样本可以提高召回率。另一方面,如果修改上下文以包含更多来自 p(x|ỹ) 的样本,其中 ỹ ≠ y,那么 Transformer 很可能输出错误的标记。这类似于上下文劫持(见第 5.5 节)。值矩阵的构造类似于 [Bietti 等人,2024; Cabannes 等人,2024] 中使用的联想记忆模型,但在我们的例子中,没有明确的一对一输入和输出对作为记忆存储。相反,输入的组合被映射到单个输出。
虽然定理 1 中的构造只是单层 Transformer 解决此任务的一种方法,但事实证明,即使在噪声情况下 (ω ≠ 1),这种 W_V 的构造也接近于训练好的 W_V. ��在第 6.1 节中,我们将证明用构造的值矩阵替换训练好的值矩阵可以保持准确性,并且构造的值矩阵和训练好的值矩阵甚至共享接近的低秩近似。此外,在这个假设模型中,部署了一个简单的均匀注意力机制,允许自注意力计算每个标记出现的次数。由于嵌入是正交向量,因此没有干扰。因此,自注意力层可以被视为聚合上下文信息。值得注意的是,在不同的设置中,需要更复杂的嵌入结构和注意力模式。这将在以下几节中讨论。✅
值矩阵的作用
定理 1 中的构造依赖于值矩阵作为联想记忆。但这是必要的吗?我们能否将值矩阵的功能集成到自注意力模块中来解决潜在概念关联问题?从经验上看,答案似乎是否定的,这将在第 6.1 节中显示。特别是,当上下文长度较小时,将值矩阵设置为单位矩阵会导致记忆召回准确率较低。
这是因为如果值矩阵是单位矩阵,Transformer 将更容易受到上下文噪声的影响。为了理解这一点,请注意,给定任何一对上下文和输出标记 (x, y),自注意力后的潜在表示 h(x) 必须位于多面体 S_y 中才能被正确分类,其中 S_y 定义为:
S_y = {v: (W_E(y) - W_E(t))^T v > 0 where t ∉ [V]∖{y}}请注意,根据定义,对于任何两个标记 y 和 ỹ,S_y ∩ S_ỹ = ∅。另一方面,由于自注意力机制,h(x) 也必须位于所有嵌入向量的凸包中:
CV = Conv(W_E(0), ..., W_E(|V|-1))换句话说,为了正确分类任何一对 (x, y),h(x) 必须位于 S_y 和 CV 的交集中。由于 x 的随机性,h(x) 很可能位于此交集之外。值矩阵的重映射效果可以帮助解决这个问题。以下引理解释了这种直觉。
引理 2
假设数据生成过程遵循第 4.1 节,其中 m ≥ 3,ω = 1,并且 𝒩(t) = {t’: DH(t, t’) = 1}。对于公式 4.1 给出的任何单层 Transformer,其中 W_E 的每一行都相互正交并归一化,如果 W_V 的构造如公式 5.1 所示,则错误率为 0。如果 W_V 是单位矩阵,则错误率严格大于 0。
当值矩阵是单位矩阵时,会出现另一个有趣的现象。在这种情况下,嵌入与其对应汉明距离之间的内积呈线性变化。这种关系可以用以下定理来形式化。
定理 3
假设数据生成过程遵循第 4.1 节,其中 m ≥ 3,ω = 1,并且 𝒩(t) = V∖{t}。对于公式 4.1 给出的任何单层 Transformer,其中 W_V 为单位矩阵,如果最小化交叉熵损失,使得对于任何采样的对 (x, y),
p(y|x) = p̂(y|x) = softmax(f_y^L(x))则存在 a > 0 和 b,使得对于两个标记 t ≠ t’,
⟨W_E(t), W_E(t')⟩ = -a DH(t, t') + b嵌入训练和几何结构
第 5.1 节中的假设模型要求嵌入形成一个正交基。在嵌入维度 d 大于标记数量 V 的过参数化机制中,可以通过高斯初始化来近似实现这一点。然而,在实践中,嵌入维度通常小于词汇量大小,在这种情况下,嵌入不可能构成这样的基。根据经验,在第 6.2 节中,我们观察到在过参数化 (d > V. 的情况下,嵌入可以冻结在其高斯初始化状态,而在欠参数化机制中,需要进行嵌入训练才能获得更好的召回准确率。✅
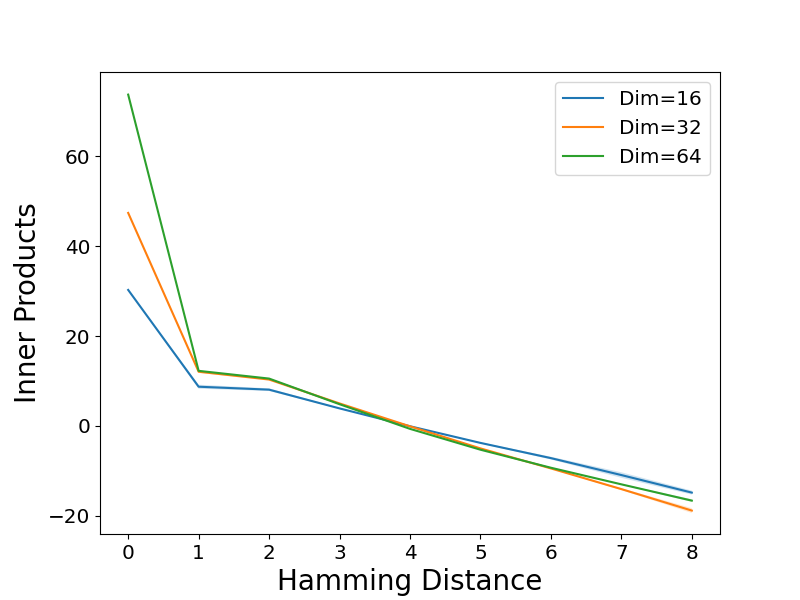
这就引出了一个问题:在欠参数化机制中学习了什么样的嵌入几何结构?实验揭示了两个标记的嵌入内积与其汉明距离之间的密切关系(见图 3(b) 和第 C. 2 节中的图 C.5)。近似地,我们有以下关系:✅
⟨W_E(t), W_E(t')⟩ = { b_0 t = t',
-a DH(t, t') + b t ≠ t'对于任意两个标记 t 和 t’,其中 b_0 > b 且 a > 0。可以将其视为高斯初始化下的嵌入几何结构与 W_V 为单位矩阵时的几何结构的组合(定理 3)。重要的是,这种结构表明训练好的嵌入本身就捕获了潜在空间内的相似性。从理论上讲,这种嵌入结构(公式 5.2)在 b_0、b 和 a 的特定条件下也可以导致低错误率,这由以下定理阐明。
定理 4(非正式)
遵循与定理 1 相同的设置,但嵌入遵循公式 5.2,那么在 a、b 的特定条件下,如果 b_0 和上下文长度 L 足够大,则错误率可以任意小,即对于任何 0 < ε < 1,R_𝒟^L(f^L. < ε。✅
定理的正式陈述及其证明在附录 A. ��定理 8)中给出。✅
值得注意的是,这种嵌入几何结构也意味着低秩结构。让我们首先考虑 b_0 = b 的特殊情况。换句话说,嵌入与其对应汉明距离之间的内积呈线性变化。
引理 5
如果嵌入遵循公式 5.2 且 b = b_0,并且 𝒩(t) = V∖{t},则 rank(W_E. ≤ m + 2。✅
当 b_0 > b 时,嵌入矩阵不会严格低秩。然而,它仍然可以表现出近似的低秩行为,其特征是顶部和底部奇异值之间存在特征间隙。这在经验上得到了验证(见第 C. 4 节中的图 C.9-C.12)。✅
注意力选择的作用
到目前为止,注意力在分析中并没有发挥重要作用。但也许并不令人意外的是,注意力机制在选择相关信息方面很有用。为了理解这一点,让我们考虑一个特定的设置,其中对于任何潜在向量 z,𝒩(z) = {z: z_1* = z_1}∖{z*}。
本质上,潜在向量根据第一个潜在变量的值被划分为两个簇,信息条件分布 π 只采样与输出潜在向量位于同一簇中的潜在向量。根据经验,当在此设置下进行训练时,注意力机制将更加关注同一簇中的标记(第 6.3 节)。这意味着自注意力层可以减轻噪声并集中于信息条件分布 π。
为了更直观地理解这一点,我们将研究未归一化注意力分数的梯度。具体来说,未归一化注意力分数定义为:
u_(t, t') = (W_K W_E(t))^T (W_Q W_E(t')) / √d_a.引理 6
假设数据生成过程遵循第 4.1 节,并且 𝒩(z) = {z: z_1 = z_1}∖{z*}。给定序列中的最后一个标记 t_L. ��则✅
∇_(u_(t, t_L. ) ℓ(f^L) = ∇ℓ(f^L)^T (W_E)^T W_V (α_t p̂_t W_E(t) - p̂_t ∑_(l=1)^L p̂_(t_l) W_E(t_l))✅其中对于标记 t,αt = ∑(l=1)^L 1[t_l = t],p̂_t 是标记 t 的归一化注意力分数。
通常,当标记 t 和 t_L 属于同一簇时,α_t 更大,因为同一簇中的标记往往频繁地共现。因此,对于同一簇中的标记,对未归一化注意力分数的梯度贡献通常更大。
上下文劫持与记忆召回的错误分类
根据潜在概念关联的理论结果,自然会产生一个问题:这些结果如何与 LLM 中的上下文劫持联系起来?本质上,对于潜在概念关联问题,输出标记的区分是通过区分各种条件分布 p(x|y) 来实现的。因此,在上下文 x 中添加或更改标记,使其类似于不同的条件分布,会导致错误分类。在第 C. 5 节中,我们展示了混合不同上下文会导致 Transformer 错误分类的实验。这部分解释了 LLM 中的上下文劫持(第 3 节)。另一方面,众所周知,错误率与上下文条件分布之间的 KL 散度有关 [Cover 等人,1999]。分布越接近,模型就越容易错误分类。这里,主要由独立同分布样本组成的较长上下文意味着更大的散度,因此记忆召回率更高。这在理论上由定理 1 和定理 4 暗示,并在第 C.6 节中得到经验证明。这一结果也与反向上下文劫持有关,在反向上下文劫持中,添加包含真实目标词的句子可以提高事实召回率。✅
实验:验证理论分析
前一节的理论结果的主要含义是:
- 值矩阵很重要,并且具有公式 5.1 中所示的联想记忆结构。
- 在欠参数化机制中,训练嵌入至关重要,其中嵌入表现出特定的几何结构。
- 注意力机制用于选择最相关的标记。
为了评估这些说法,我们在合成数据集上进行了几项实验。其他实验细节和结果可以在附录 C 中找到。
关于值矩阵 W_V
在本节中,我们将研究值矩阵 W_V 的必要性及其结构。首先,我们进行实验来比较训练和冻结 W_V 为单位矩阵的影响,上下文长度 L 设置为 64 和 128。图 3(a) 和图 C. 1 显示,当上下文长度较小时,冻结 W_V 会导致准确率显著下降。这与引理 2 一致,并在一般情况下对其进行了验证,这意味着值矩阵在保持高记忆召回率方面的重要性。✅
接下来,我们研究训练好的值矩阵 W_V 与公式 5.1 中构造的值矩阵之间的一致程度。第一组实验检查了两个矩阵在功能上的相似性。我们将训练好的 Transformer 中的值矩阵替换为公式 5.1 中构造的值矩阵,然后报告使用新值矩阵的准确率。作为基线,我们还考虑随机构造的值矩阵,其中外积对是随机选择的(详细构造可以在第 C. 1 节中找到)。图 C.2 表明,当值矩阵被替换为构造的值矩阵时,准确率并没有显著下降。此外,构造的值矩阵和训练好的值矩阵不仅在功能上相似,而且它们还共享相似的低秩近似。我们使用奇异值分解来获得各种值矩阵的最佳低秩近似,其中秩设置为与潜在变量的数量 (m) 相同。然后,我们计算训练好的值矩阵的低秩近似与构造的、随机构造的和高斯初始化的值矩阵的低秩近似之间的最小主角度。图 C.3 显示,构造的值矩阵平均而言与训练好的值矩阵具有最小的主角度。✅
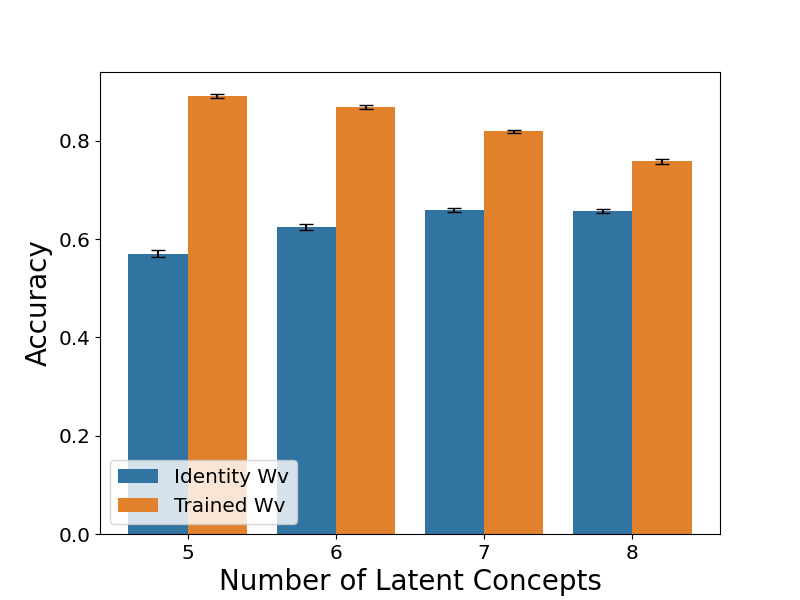
图 3:单层 Transformer 的关键组件在潜在概念关联问题上协同工作。(a) 与训练
W_V 相比,将值矩阵 W_V 固定为单位矩阵会导致准确率降低。该图报告了 L =
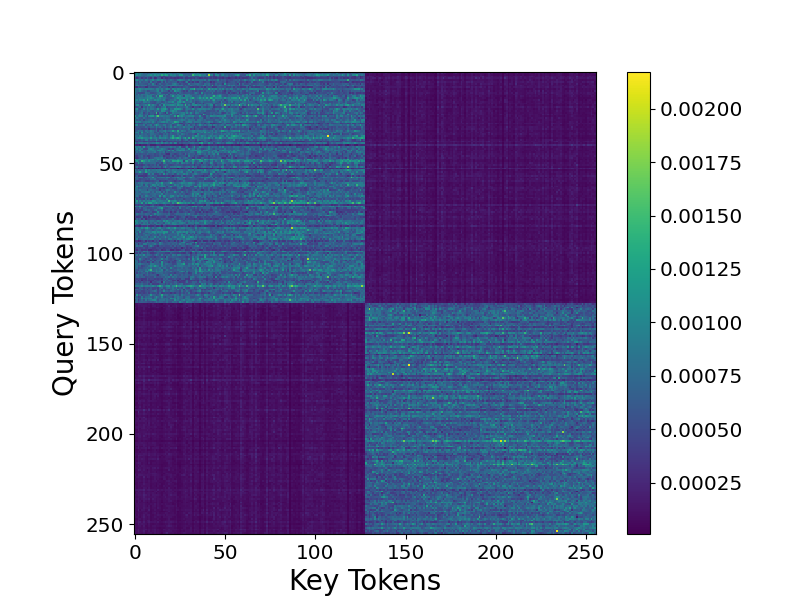
64 时固定和训练 W_V 的平均准确率。(b) 在欠参数化机制中进行训练时,嵌入结构由公式 5.2 近似。该图显示了当 m = 8 时,两个标记的嵌入之间的平均内积与其对应汉明距离的关系。(c) 自注意力层可以选择同一簇中的标记。该图显示了 m = 8 时的平均注意力分数热图和第 5.4 节中的簇结构。
关于嵌入
在本节中,我们将探讨嵌入训练在欠参数化机制中的重要性以及嵌入结构。我们进行实验来比较训练和冻结嵌入在不同嵌入维度下的影响。根据维度,从 {0.01, 0.001} 中选择最佳学习率。图 C. 4 清楚地表明,当维度小于词汇量大小 (d < V) 时,需要进行嵌入训练。在过参数化机制 (d > V) 中,这不是必需的,这部分证实了定理 1,因为如果嵌入是从高维多元高斯分布初始化的,它们近似相互正交并具有相同的范数。✅
下一个问题是在欠参数化机制中,训练好的 Transformer 形成了什么样的嵌入结构。从图 3(b) 和图 C. 5 可以明显看出,两个标记的嵌入的平均内积与其对应汉明距离之间的关系大致符合公式 5.2。也许令人惊讶的是,如果我们绘制值矩阵固定为单位矩阵的训练好的 Transformer 的相同图形,则关系大多是线性的,如图 C.6 所示,这证实了我们的理论(定理 3)。✅
正如第 5.3 节所建议的那样,这种嵌入几何结构(公式 5.2)会导致低秩结构。我们通过研究嵌入矩阵 W_E 的谱来验证这一说法。如图 C. 4 所示,图 C.9-C.12 表明顶部和底部奇异值之间存在特征间隙,表明存在低秩结构。✅
关于注意力选择机制
在本节中,我们将通过考虑第 5.4 节中定义的一类特殊的潜在概念关联模型来研究注意力模式的作用。图 3(c) 和图 C. 7 清楚地表明,自注意力选择了与最后一个标记位于同一簇中的标记。这表明注意力可以过滤掉噪声并集中于信息条件分布 π。我们将实验扩展到考虑依赖于前两个潜在变量的簇结构(详细构造可以在第 C.3 节中找到),图 C.8 显示了预期的注意力模式。✅
结论:对LLM内部机制的进一步理解
在这项工作中,我们首先介绍了 LLM 中的上下文劫持现象,这表明事实检索对于上下文的变异并不鲁棒。这表明 LLM 可能像联想记忆一样工作,其中上下文中的标记是引导记忆检索的线索。为了进一步研究这一观点,我们设计了一个名为潜在概念关联的合成任务,并从理论上和经验上研究了如何训练单层 Transformer 来解决此任务。这些结果为 Transformer 和 LLM 的内部工作机制提供了进一步的见解,并有望激发进一步的工作来解释和理解 LLM 预测标记和回忆事实的机制。
参考文献
- Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A., et al. (2020). Language models are few-shot learners. Advances in neural information processing systems, 33:1877–1901.✅
- Meng, K. , Bau, D., Andonian, A., and Belinkov, Y. (2022). Locating and editing factual associations in gpt. Advances in Neural Information Processing Systems, 35:17365–17380.✅
- Meng, K. , Lee, D., Bau, D., and Belinkov, Y. (2023). Mass-editing factual associations in language models. arXiv preprint arXiv:2303.08354.✅
- De, A. , Burns, C., Malinowski, M., and Rumshisky, A. (2021). Editing factual knowledge in language models. arXiv preprint arXiv:2112.08155.✅
- Mitchell, E. , Lin, C.-J., Bosselut, A., Finn, C., and Manning, C. D. (2021). Fast model editing at scale. arXiv preprint arXiv:2110.11309.✅
- Mitchell, E. , Lee, K., Khabsa, M., Lin, C.-J., Finn, C., and Manning, C. D. (2022). Memory-based model editing at scale. arXiv preprint arXiv:2207.14296.✅
- Dai, D. , Dong, L., Hao, Y., Sui, Z., Ke, F., Zhang, J., Zhang, Y., Wang, J., and Qiu, X. (2021). Knowledge neurons in pretrained transformers. arXiv preprint arXiv:2104.08688.✅
- Radford, A. , Wu, J., Child, R., Luan, D., Amodei, D., and Sutskever, I. (2019). Language models are unsupervised multitask learners. OpenAI blog, 1(8):9.✅
- Team, G. (2024). Gemma.✅
- Touvron, H. , Martin, L., Stone, K., Albert, P., Almahairi, A., Babaei, Y., Bashlykov, N., Batra, S., Bhargava, P., Bhosale, S., et al. (2023). Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.✅
- Zhao, W. , Peng, B., Zhou, C., Wang, J., and Chang, S. (2023). Context-aware prompt learning for few-shot text classification. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 6436–6448.✅
- Firth, J. R. (1957). A synopsis of linguistic theory, 1930–1955. Studies in linguistic analysis.✅
- Li, Z. , Wallace, E., Shen, S., Lin, K., Ke, G., and Zhang, S. (2023). Transformers learn in-context by gradient descent. arXiv preprint arXiv:2308.12175.✅
- Tarzanagh, D. A. and Dasgupta, S. (2023). Margin maximization in transformers for in-context few-shot learning. arXiv preprint arXiv:2305.11146.✅
- Li, Z. , Wallace, E., Shen, S., Lin, K., Ke, G., and Zhang, S. (2024). The mechanics of in-context learning in transformers. arXiv preprint arXiv:2401.04182.✅
- Cover, T. M. (1999). Elements of information theory. John Wiley & Sons.✅
- Devroye, L. , Lugosi, G., and Boucheron, S. (2013). A probabilistic theory of pattern recognition, volume 31. Springer Science & Business Media.✅
- Loshchilov, I. and Hutter, F. (2017). Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101.✅
