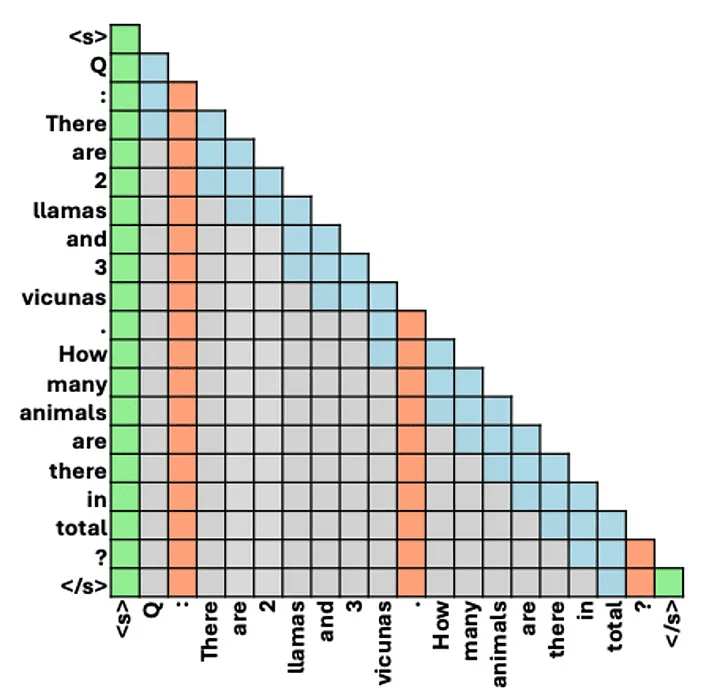
循环神经网络(RNNs)长期以来一直是处理时间序列数据的经典架构。然而,RNN在长序列训练中面临的一个主要难题就是梯度的消失和爆炸。尽管近年来状态空间模型(SSMs),作为RNN的一种子类,成功解决了这些问题,但它们的成功却挑战了我们对理论的理解。本文将深入探讨RNN的优化挑战,并发现随着网络记忆的增加,参数变化会导致输出变化剧烈,即使没有梯度爆炸,基于梯度的学习仍然非常敏感。我们的分析还揭示了元素级递归设计模式结合细致参数化在缓解这一问题中的重要性。这一特性存在于SSMs以及其他架构,如LSTM中。总体而言,我们的见解为RNN基于梯度学习的一些困难提供了新的解释,并解释了为什么某些架构比其他架构表现更好。
循环神经网络的挑战
循环神经网络(RNN)在处理时间序列数据方面表现出色,但它们在训练长序列时面临显著挑战,主要是因为误差信号在时间反向传播过程中会消失或爆炸。注意力机制(如Transformer中所用)通过允许直接的token-to-token通信,极大地简化了长时间间隔内的信号传播,解决了这些问题。然而,Transformer的性能提升伴随着计算和内存消耗的增加,这激发了大量研究以提高其效率。
一种有前景的研究方向是线性递归网络的新类型,即状态空间模型(SSMs)。这些模型以更快的训练速度换取表达能力的降低,并已被证明在捕捉长程依赖性方面特别有效。我们在本文中探讨这种有效性是否仅仅归因于它们避免了梯度消失和爆炸。由于这些模型的简单性,它们为深入的理论分析提供了机会。我们重点研究这些模型中的信号传播。
在回顾经典的RNN结果后,我们发现它们会遭遇一个被忽视的问题:记忆的诅咒。当递归网络编码更长的记忆时,网络活动对参数变化变得极其敏感,即使网络动态保持稳定。在第三部分,我们展示了SSMs及其他架构如LSTM如何有效地缓解这一问题。最后,我们通过分析一个简单的教师-学生任务,揭示了线性递归网络学习的复杂性,并讨论了我们的发现如何扩展到更现实的场景。
消失和爆炸梯度问题
首先介绍我们将在本文中使用的符号。我们考虑一个具有隐藏状态 $h_t$ 的循环神经网络,更新函数 $f_\theta$ 由参数 $\theta$ 参数化,以及输入序列 $(x_t)_t$。网络的平均性能通过损失 $L$ 来衡量。我们有:
瞬时损失 $L_t$ 相对于参数 $\theta$ 的梯度等于:
早期研究指出,梯度下降很难让RNN记住将来有用的过去输入,因为误差信号在时间反向传播过程中要么消失要么爆炸。关键的量是:
当雅可比矩阵 $\frac{\partial h_{i+1}}{\partial h_i}$ 的谱半径小于1时,这个量会指数级收敛到0;如果存在大于1的分量,它会指数级爆炸。随着时间跨度的增加,过去隐藏状态对当前损失的贡献变得要么可忽略不计,要么占主导地位,这使得基于梯度的长期记忆学习变得困难。
记忆的诅咒
解决了消失和爆炸梯度问题后,RNN是否就能顺利学习长程依赖了呢?我们发现并非如此。即使动态稳定,随着网络记忆的增加,梯度仍可能爆炸。
直观理解
RNN的特殊之处在于同一个更新函数 $f_\theta$ 被反复应用。因此,修改参数不仅影响单次更新,而是所有更新。随着网络记忆的增加,隐藏状态对参数变化变得越来越敏感,即使没有梯度爆炸,学习参数仍变得更加困难,这就是记忆的诅咒。
线性对角递归神经网络中的信号传播
我们研究了在编码长程依赖时,隐藏状态和梯度幅度如何演变。理想情况下,这些量不应消失或爆炸。我们做了以下假设:
- 线性对角递归神经网络:我们限制更新函数为$f_\theta(h_t, x_{t+1}) = \lambda \odot h_t + x_{t+1}$,其中$\lambda$是与$h_t$同维的向量,$\odot$表示元素级乘积。
- 无限时间视角:考虑无限序列,并在$t_0 = -\infty$初始化网络动态。
- 广义平稳:假设网络接收的不同量(包括输入$x_t$)是广义平稳的,即自相关函数与时间无关。
在这些假设下,我们分析了单层递归网络中的信号传播,发现当$|λ| \to 1$时,隐藏状态和反向传播的误差都会爆炸。
缓解记忆的诅咒
给定这一问题,如何缓解呢?对角连接的递归网络特别适合。除了避免梯度爆炸,它们还通过输入归一化和重新参数化来缓解记忆的诅咒。
解决方案:归一化和重新参数化
通过引入输入归一化和重新参数化,我们可以保持隐藏状态和梯度的幅度稳定。例如,为了保持$E[h_t^2]$和$E[(d_\lambda h_t)^2]$独立于$\lambda$,我们可以引入一个归一化因子$\gamma(\lambda)$,并选择适当的参数化方式来控制$\lambda$。
复杂数的情况
对于复杂数$\lambda$,合适的参数化更加困难。我们的分析表明,若$\lambda$参数化为$\nu \exp(i\theta)$,则$\theta$的参数化必须依赖于$\nu$,但反之不然。尽管如此,这种参数化并不会妨碍学习。
多种RNN架构的比较
状态空间模型和门控RNN都具有某种形式的归一化和重新参数化机制,有助于信号传播。我们比较了这些机制在不同架构中的作用,发现状态空间模型和门控RNN在缓解记忆的诅咒方面表现出色。
线性教师-学生分析
我们考虑一个教师-学生任务,教师和学生都是线性递归网络。尽管这是最简单的设置,但它揭示了RNN学习中的复杂性。通过一维和多维情况的实验,我们发现对角化显著简化了优化过程,并且自适应学习率对缓解记忆的诅咒至关重要。
自适应学习率的重要性
自适应学习率可以有效应对梯度的爆炸。我们分析了损失函数的Hessian矩阵,发现对角化结构有助于自适应优化器更好地处理较大的曲率,从而加速学习。
深度递归网络中的信号传播
我们进一步验证了理论趋势在实际中的适用性。通过在深度递归网络中初始化信号传播,实验结果验证了复杂数RNN、LRU和LSTM在不同记忆长度下的表现。我们发现LRU在前向和反向传递中几乎完全缓解了记忆的诅咒,而LSTM则通过特定参数化保持了梯度的稳定。
结论
梯度消失和爆炸使得RNN的学习变得复杂,但解决这些问题并非终点。我们发现,RNN的迭代特性在动态稳定的边缘引发了另一个学习困难。通过重新参数化和自适应学习率可以有效缓解这一问题,而对角化递归简化了优化过程。我们的分析还揭示了学习复杂数特征的复杂性,这可能解释了为什么复杂数在最新的状态空间模型架构中并不常见。
未来研究可以进一步探索如何在保持良好优化特性的同时,提高小型线性模块的表达能力。理解模块化设计在不同场景中的应用,可能会为构建更高效和强大的神经网络提供新的思路。