突破强化学习瓶颈：Group Relative Policy Optimization (GRPO) 的设计与实现

强化学习（Reinforcement Learning, RL）近年来在大规模语言模型（LLM）优化中扮演了重要角色。然而，传统的强化学习方法如 Proximal Policy Optimization (PPO) 在大规模模型训练中面临显著的计算瓶颈和复杂性挑战。为了解决这些问题，DeepSeek-AI 团队提出了一种高效且创新的强化学习算法——Group Relative Policy Optimization (GRPO)。GRPO 不仅显著降低了训练资源需求，还在数学推理任务中展现了卓越的性能提升。本文将聚焦 GRPO 的核心设计与实现，深入剖析其算法细节与技术创新。

背景与挑战：为什么需要 GRPO？

1. PPO 的局限性

PPO 是当前 LLM 强化学习中的主流方法，其目标是通过限制策略更新的幅度，确保训练的稳定性。PPO 的优化目标如下：
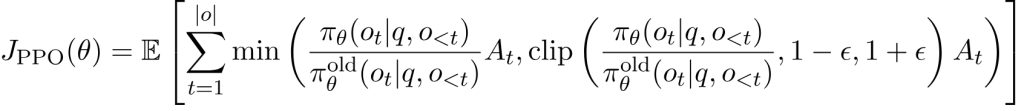
$$J_{\text{PPO}}(\theta) = \mathbb{E}\left[\sum_{t=1}^{|o|} \min\left(\frac{\pi_\theta(o_t | q, o_{<t})}{\pi_\theta^{\text{old}}(o_t | q, o_{<t})} A_t, \text{clip}\left(\frac{\pi_\theta(o_t | q, o_{<t})}{\pi_\theta^{\text{old}}(o_t | q, o_{<t})}, 1-\epsilon, 1+\epsilon\right) A_t\right)\right]$$
其中：

$\pi_\theta$ 和 $\pi_\theta^{\text{old}}$ 分别是当前策略和旧策略。
$A_t$ 是优势函数（Advantage Function），由 Generalized Advantage Estimation (GAE) 计算。

尽管 PPO 在稳定性上表现优异，但其在大规模模型训练中的局限性不容忽视：

高计算成本：PPO 需要一个与策略模型规模相当的价值函数模型（critic model），这对内存和计算资源提出了极高要求。
训练复杂性：价值函数的训练依赖于每个 token 的奖励信号，而奖励模型通常只对最后一个 token 打分。这种不匹配可能导致价值函数的误差积累，影响训练效果。

2. GRPO 的设计目标

为了解决上述问题，GRPO 的设计目标是：

去除价值函数：通过组内奖励的相对比较，替代传统的价值函数，降低计算资源需求。
简化训练流程：减少对复杂奖励建模的依赖，直接使用组内相对奖励进行优化。
提升性能：在减少计算成本的同时，确保模型在推理任务中的性能提升。

GRPO 的核心设计与实现

GRPO 的核心思想是通过组内相对奖励（Group Relative Reward）优化策略模型，避免了传统 PPO 对价值函数的依赖。以下是 GRPO 的完整实现细节。

1. 组内奖励建模

在 GRPO 中，每个问题 $q$ 的奖励信号来源于组内多个输出的相对比较。具体步骤如下：

采样组内输出
对于每个问题 $q$，从旧策略 $\pi_\theta^{\text{old}}$ 中采样一组输出 ${o_1, o_2, \dots, o_G}$。
计算组内奖励
使用奖励模型对每个输出 $o_i$ 进行评分，得到奖励 ${r_1, r_2, \dots, r_G}$。
归一化奖励
计算组内奖励的均值和标准差，并将奖励归一化为组内相对奖励：
$$A_i = \frac{r_i – \text{mean}({r_1, r_2, \dots, r_G})}{\text{std}({r_1, r_2, \dots, r_G})}$$

2. 优化目标

GRPO 的优化目标函数如下：
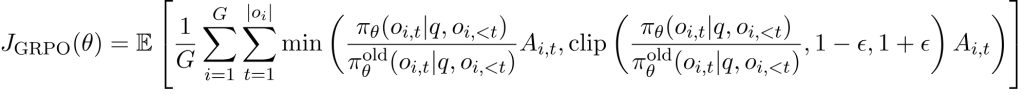
$$J_{\text{GRPO}}(\theta) = \mathbb{E}\left[\frac{1}{G} \sum_{i=1}^G \sum_{t=1}^{|o_i|} \min\left(\frac{\pi_\theta(o_{i,t} | q, o_{i,<t})}{\pi_\theta^{\text{old}}(o_{i,t} | q, o_{i,<t})} A_{i,t}, \text{clip}\left(\frac{\pi_\theta(o_{i,t} | q, o_{i,<t})}{\pi_\theta^{\text{old}}(o_{i,t} | q, o_{i,<t})}, 1-\epsilon, 1+\epsilon\right) A_{i,t}\right)\right]$$
其中：

$A_{i,t}$ 是第 $i$ 个输出的第 $t$ 个 token 的优势值，等于组内相对奖励 $A_i$。
$\epsilon$ 是用于限制策略更新幅度的超参数。

3. KL 正则化

为了进一步稳定训练过程，GRPO 在目标函数中加入了 KL 散度正则化项：
$$D_{\text{KL}}(\pi_\theta || \pi_{\text{ref}}) = \sum_{o_i} \pi_\theta(o_i | q) \log\left(\frac{\pi_\theta(o_i | q)}{\pi_{\text{ref}}(o_i | q)}\right)$$
其中，$\pi_{\text{ref}}$ 是参考策略模型（通常是初始的 SFT 模型）。

最终的优化目标为：
$$J_{\text{GRPO}}(\theta) = J_{\text{GRPO}}(\theta) – \beta D_{\text{KL}}(\pi_\theta || \pi_{\text{ref}})$$
其中，$\beta$ 是 KL 正则化项的权重。

GRPO 的实现与训练流程

以下是 GRPO 的完整训练流程：

1. 初始化

使用监督微调（SFT）模型作为初始策略模型 $\pi_\theta$。
初始化奖励模型 $r_\phi$，用于对输出进行评分。

2. 采样与奖励计算

从当前策略模型 $\pi_\theta$ 中采样一组输出 ${o_1, o_2, \dots, o_G}$。
使用奖励模型对每个输出进行评分，计算组内奖励 ${r_1, r_2, \dots, r_G}$。
归一化奖励，得到组内相对奖励 ${A_1, A_2, \dots, A_G}$。

3. 策略优化

使用组内相对奖励作为优势值，计算 GRPO 的目标函数。
通过梯度下降优化策略模型 $\pi_\theta$。

4. 迭代式更新

定期更新参考模型 $\pi_{\text{ref}}$，使其与当前策略模型保持一致。
使用策略模型生成的新数据持续训练奖励模型 $r_\phi$。

实验与结果分析

在数学推理任务中，GRPO 展现了显著的性能提升。以下是基于 GRPO 的实验结果：

数学基准测试
在 GSM8K 和 MATH 数据集上，基于 GRPO 的 DeepSeekMath-RL 7B 分别达到了 88.2% 和 51.7% 的准确率，显著优于所有开源模型。
计算效率
GRPO 通过去除价值函数，减少了约 40% 的内存消耗，同时训练速度提升了约 30%。
稳定性
GRPO 的 KL 正则化项有效抑制了策略模型的过度更新，确保了训练过程的稳定性。

GRPO 的优势与未来展望

1. GRPO 的优势

高效性：通过组内奖励替代价值函数，显著降低了计算成本。
易实现：算法设计简洁，易于集成到现有的 LLM 强化学习框架中。
性能优越：在数学推理任务中展现了卓越的性能提升。

2. 未来改进方向

奖励模型的泛化能力：探索更强大的奖励模型，以适应更复杂的任务。
多任务扩展：将 GRPO 应用于其他领域，如代码生成和逻辑推理。
大规模模型验证：在更大规模的模型（如 70B 参数）上验证 GRPO 的性能。

结语

GRPO 的提出为大规模语言模型的强化学习开辟了一条新路径。通过组内相对奖励的创新设计，GRPO 在显著降低计算成本的同时，实现了卓越的性能提升。这一算法不仅为数学推理任务设立了新的标杆，也为强化学习在语言模型中的应用提供了重要启示。未来，随着算法的进一步优化与扩展，GRPO 有望在更多领域展现其潜力。

突破强化学习瓶颈：Group Relative Policy Optimization (GRPO) 的设计与实现 New