在多智能体强化学习 (MARL) 中,准确感知对手的策略对于合作和对抗环境都至关重要,尤其是在动态环境中。虽然 Proximal Policy Optimization (PPO) 和类似算法(如 Actor-Critic with Experience Replay (ACER)、Trust Region Policy Optimization (TRPO) 和 Deep Deterministic Policy Gradient (DDPG))在单智能体静态环境中表现出色,但在 MARL 中由于对手的非平稳和隐藏策略,它们会遭受高方差,导致奖励性能下降。此外,现有的 MARL 方法面临着重大挑战,包括需要智能体间通信、依赖显式奖励信息、高计算需求和采样效率低下。这些问题使得它们在对手可能突然改变策略而没有事先通知的连续环境中效率低下。
针对上述背景,我们提出了一种名为 OPS-DeMo(在线策略切换检测模型)的在线算法,该算法利用动态误差衰减来检测对手策略的变化。OPS-DeMo 通过一个假设对手策略 (AOP) 库不断更新其信念,并从一个预先训练的响应策略库中选择相应的响应。每个响应策略都针对持续策略化对手进行训练,减少训练不确定性,并使 PPO 等算法能够在多智能体环境中有效使用。比较评估表明,我们的方法在捕食者-猎物设置等动态场景中优于 PPO 训练的模型,为突然的策略转变提供了更大的鲁棒性,并通过精确的对手策略洞察,使决策更明智。
对手策略切换检测的必要性
现实世界中的智能体在处理多个实体之间的互动时面临着重大挑战,而人类却能轻松应对。例如,足球运动员必须预测队友的移动,每个队友都有不同的角色和技能,以及对手;自动驾驶汽车需要预测道路上其他车辆的多样化行为。这些互动涉及不同的行为,需要不同的策略才能获得最佳结果。这些实体被称为对手,从分散式智能体的角度来看,它们创造了一个非平稳的环境。
在正常情况下,对手或交互实体的策略通常是隐藏的。尽管交换策略可能带来潜在的好处,但频繁的通信并不总是可行的,对手可能不愿意分享他们的策略,这阻碍了直接的学习机会。因此,需要通过实时观察对手的行为来更新我们对对手策略的信念。然而,仅仅依靠过去的观察可能会存在问题,因为这些观察可能无法准确反映当前的策略,因为对手的学习过程存在随机波动或适应性。通过更加重视最近的行为,我们可以逐渐收敛到理解他们真正的当前策略。然而,对手策略的突然转变可能会发生,导致准确跟踪其策略的挑战。未能检测到这些突然的变化会减慢学习进度,并阻碍智能体有效适应的能力。例如,在分析金融市场时,玩家的策略通常没有明确表达,并且基于各种因素(从小到大),市场的环境可能会突然发生变化。
传统方法的局限性
为了有效地与其他智能体互动,需要理解他们的行为和决策,这个过程可以通过对手建模来帮助实现,对手建模是指构建和使用对手行为模型。理想情况下,对手模型有助于提取对手策略,帮助制定利用对手弱点策略。然而,由于智能体行为的动态性,这种建模具有挑战性。非平稳行为需要不断更新学习到的对手模型。例如,在足球比赛中,后卫可以在反击中变成进攻队员,从而显著改变他们的策略。类似地,自动驾驶汽车可能会根据对环境变化的信念调整其策略。
为了解决上述问题,强化学习是一种用于策略学习的范式,它专注于智能体通过与环境的试错来最大化长期累积奖励[4]。虽然在单智能体环境中有效,但在多智能体环境中由于智能体的非平稳性而难以实现。常见的强化学习算法,如 DQN、DDPG、AAC 和 PPO,经过优化,能够在称为马尔可夫决策过程 (MDP) 的静态环境中获得高奖励。然而,当应用于多智能体 MDP 时,多个智能体相互作用,这些算法由于其他智能体策略的逐渐或突然变化而导致方差增加,从而面临挑战。
几种针对多智能体场景量身定制的算法,如 BPR+[5]、DPN-BPR+[6]、LOLA[7] 和 meta-MAPG[8],通过各种策略来应对非平稳环境的挑战。LOLA 旨在影响对手的行为,而 Meta-MAPG 则专注于元学习环境动态。BPR+ 和 DPN-BPR+ 利用先前学习到的响应策略,假设对手的非平稳性不频繁,类似于对手之间偶尔的切换。然而,LOLA 和 Meta-MAPG 不适合对手策略的突然转变。相比之下,BPR+ 和 DPN-BPR+ 依赖于奖励信号来检测对手策略的转变,这限制了它们在具有持续奖励数据的片段环境中的有效性,在连续环境中准确检测突然的策略切换方面存在挑战。
OPS-DeMo 的创新之处
需要一种有效的方法来仅基于观察到的行为来检测策略切换,尤其是在传统统计方法在对手轨迹短暂的场景中效果不佳的情况下。SAM(切换智能体模型)通过估计假设策略的运行误差来解决这个问题,防止智能体遵循假设策略时误差无限增加。然而,SAM 是针对确定性动作量身定制的,通常与 DDPG [9] 配合使用,并且缺乏对运行误差衰减的详细公式。
OPS-DeMo 的核心思想
为了总结这项工作的主要贡献,我们重点介绍以下几点:
- 我们引入了一个运行误差估计指标来评估智能体对随机策略的遵守程度,仅利用轨迹中观察到的状态-动作对。该指标在线运行,并且可以随着新观察结果的处理而不断更新,而无需存储。
- 此外,我们提出了一种在线算法,该算法利用运行误差估计指标来检测对手的策略切换,并相应地调整响应策略。
- 通过对我们提出的算法与当前最先进算法进行严格的比较分析,我们评估了这些提议的优点并对其进行了介绍。
OPS-DeMo 的算法细节
在本节中,我们介绍了我们提出的解决第 2 节中讨论的问题的方案。首先,我们介绍了一种新的指标来衡量智能体对策略的遵守程度,该指标基于其最近的行为。该指标可以在运行时使用,并在第 3.1 节中详细说明。接下来,我们在第 3.2 节中描述了我们提出的模型的架构。最后,我们在第 3.3 节中介绍了一种专门针对对手行为变化进行调整的算法。
3.1 衡量策略遵守程度的指标
检测策略在马尔可夫状态之间具有近似均匀的动作概率分布的遵守情况,存在重大挑战,尤其是在以短轨迹为特征的环境中。传统的基于频率分布的方法通常效果不佳,因为它们需要频繁地重新访问状态,而这种条件在数据可用性有限的情况下是不切实际的。一种更可行的方法是将观察到的动作与其预期概率进行比较,并实时计算误差指标。如果此误差超过预先定义的阈值,则表明可能偏离策略。然而,为了减轻由于固有随机性而导致的误差累积,实施衰减机制至关重要。
这种衰减机制应该考虑智能体遵循策略时和偏离策略时的预期误差。通过结合这种衰减,该方法旨在防止误差无限期地升级,尤其是在智能体真正遵循具有固有采样误差的随机策略的情况下。假设一个具有离散动作空间的 MDP 的策略为 π。在给定的马尔可夫状态 s 中,策略 π 可以根据公式 1 写成。这里,pai 表示从状态 s 中选择动作 ai 的概率。
π(s) = (pa1 , pa2 , pa3 , . . . pai , . . . , pan) (1)
类似地,给定马尔可夫状态 s 中动作的观察频率可以根据公式 2 写成。在公式 2 中,当选择动作 ai 时,fai 设置为 1。否则,它将设置为 0。
fo(s) = (fa1 , fa2 , fa3 . . . fai , . . . , fan) (2)
现在,基于公式 1 和 2,假设智能体遵循策略 π,则在状态 s 中观察到的误差可以写成:
eo(π, s) = 1/2 * Σ(k=1 to n) |π(s) – fo(s)|ak (3)
现在,我们陈述一些引理来讨论与公式 3 相关的某些特征。
引理 1: 考虑一个具有 n 个动作的离散动作空间的 MDP 中的时间步长 t,其中一个智能体遵循策略 π 并从马尔可夫状态 s 中选择动作 ai。在此框架中,t 处的观察误差可以表示为 (1 – pai),其中 pai 表示随机策略 π 选择动作 ai 的概率。
证明: 让我们检查每个动作的观察频率,注意到除了 ai 之外的所有动作的频率都为 0。因此,观察到的误差可以表示如下:
eo(π, s) = 1/2 * [|0 – pa1| + |0 – pa2| + |0 – pa3| + . . . |1 – pai| + |0 – pai+1| + . . . + |0 – pan|] (根据公式 3)
= 1/2 * [pa1 + pa2 + pa3 + . . . + (1 – pai) + pai+1 + . . . pan] (因为,任何 0 ≤ pai ≤ 1)
= 1/2 * [(1 – pai) + (1 – pai)] (因为,任何 Σ(j=1 to n) paj = 1 ⇒ pai = 1 – Σ(k=1,k≠i to n) pak)
= (1 – pai) (4)
由于观察到的误差 eo(π, s) 是由于所选动作 a 引起的,因此在本讨论中,我们还使用 eo(π, s, a) 来表示在策略 π 下,由于状态 s 中的动作 a 而导致的类似观察误差。
引理 2: 在一个具有 n 个动作的离散动作空间的 MDP 中,考虑一个时间步长 t,其中一个智能体遵循策略 π,并且系统处于马尔可夫状态 s。在此框架中,t 步长中从策略 π 自然发生的预期误差可以表示为 Σ(j=1 to n) paj (1 – paj)。这里,paj 表示根据随机策略 π 选择动作 aj 的概率。
证明: 当智能体遵循策略 π 时,选择动作 ai 的概率为 pai,这会导致观察到的误差 (1 – pai)(引理 1)。因此,遵循策略 π 时的预期误差为:
E[eo(π, s) | π] = Σ(j=1 to n) paj (1 – paj) (5)
引理 3: 在一个具有 n 个动作的离散动作空间的 MDP 上下文中,考虑一个时间步长 t,其中一个智能体遵循除特定策略 π 之外的任何策略 φ,并且系统处于马尔可夫状态 s。在此框架中,t 处从策略 π 自然发生的预期误差可以表示为 (n-1)/n。
证明: 考虑智能体偏离策略 π 而是遵循另一种但未知的策略 φ 的情况。在这种情况下,智能体在不遵循策略 π 时选择任何动作的概率在所有动作之间均匀分布,尽管策略 φ 下的特定分布仍然未知。因此,在不遵循策略 π 时,从策略 π 观察到的预期误差可以表示为公式 6。这里,πc 表示特定问题的所有可能策略的集合。
E[eo(π, s) | φ ∈ πc] = Σ(j=1 to n) 1/n * (1 – paj) = (n-1)/n (6)
3.2 模型架构
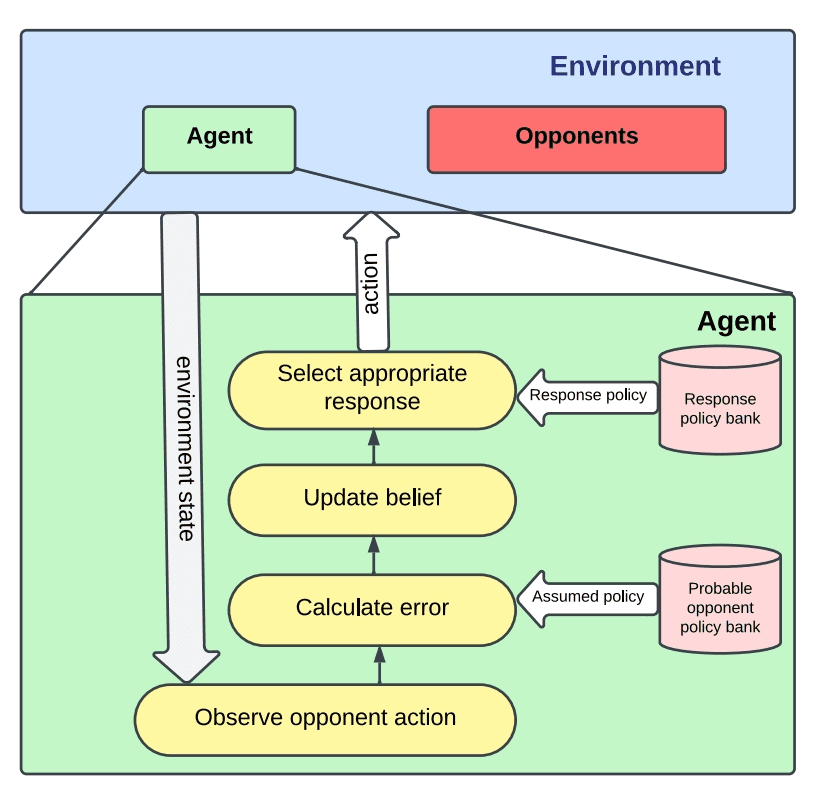
在由具有离散动作空间的 MDP 建模的给定环境中,我们采用了一种策略,针对每个可能的对手策略 Φi ∈ Πo 训练响应策略 πi,其中 Πo 表示包含各种可能的对手策略的策略库。响应策略的训练涉及使用最先进的学习算法,如 PPO。在训练过程之后,我们的智能体准备好在环境中部署。结合所有想法,我们在图 1 中给出了我们提出的 OPS-DeMo 架构的高级概述。
在任何给定的时刻,当对手被假定为遵循特定策略 φi 并且被观察到选择动作 aj 时,我们利用策略库 Πo 来确定每个可能的对手策略选择观察到的动作的概率。随后,我们计算相应的观察误差,并利用指定的算法更新我们对当前对手策略的信念。在更新信念之后,我们选择一个合适的响应策略,并根据所选响应策略确定智能体的动作。这种迭代过程使我们的智能体能够在部署期间动态地适应遇到的各种对手策略。

[图片:OPS-DeMo 架构图]
3.3 算法描述
我们提出了一种算法(算法 1),用于运行误差估计(第 8-17 行)、策略切换检测(第 18-19 行)和调整响应策略(第 20-21 行)。该算法根据对手当前策略的更新信念,利用已经训练好的对手策略库 Πo 和 PPO 训练的响应策略库 ρ 来最大化累积奖励。该算法使用提供的运行误差估计方法来查看 Πo 中的哪个策略更符合对手的最近行为,然后选择运行误差最小的策略,并采取适当的响应策略,以在当前场景中最大化奖励。

3.4 策略切换检测
我们使用观察到的误差来为对手策略库 Πo 中的每个策略累积运行误差(参考算法 1,第 8-24 行)。如果当前假设的对手策略 Φ 的运行误差超过阈值,我们假设对手在此期间切换了其策略。然而,自然发生的误差可能会使运行误差无限增大。因此,运行误差的衰减方法至关重要。
3.5 误差衰减
对于给定的马尔可夫状态 s,遵循策略 Φ 时的预期误差表示为 ef(参考公式 5),而未遵循策略 Φ 时的预期误差表示为 enf(参考公式 6),则这两个值之间的衰减由公式 7 定义。这里,φc 表示特定问题的所有可能策略的集合。
d = αef + (1 – α)enf = αE[eo(Φ, s)] + (1 – α)Eeo(Φ, s) | φ′ ∈ Φc
在此公式中,参数 α ∈ [0, 1] 表示衰减的严格性系数。较高的 α 值意味着更严格的检测模型,不允许与假设策略类似但没有显著差异的策略。相反,较低的 α 值允许更宽松的方法。仔细选择 α 在将检测模型定制到特定需求方面至关重要。
这种衰减可以防止运行误差无限增长,并且是动态计算的(参考算法 1,第 10 行)。
3.6 切换后策略的识别
为了有效地重用训练好的响应策略,识别对手切换后的策略成为一项关键任务。我们建议维护所有潜在对手策略的运行误差记录。当当前假设的策略的运行误差超过预定的阈值时,当前运行误差最小的策略被指定为切换的策略。随后,运行误差减半,以减轻过度频繁切换的发生(参考算法 1,第 22 行)。这种方法旨在提高动态环境中策略检测的鲁棒性和稳定性。
实验评估
在本节中,我们通过将 OPS-DeMo 与当前最先进的学习算法进行比较,使用各种指标来评估其在马尔可夫博弈(捕食者-猎物)中的性能。此分析的关键指标包括累积奖励和对手策略假设的准确性。这种评估旨在专门评估运行误差估计方法在对手策略频繁变化和不同严格性水平下的有效性。
与传统的学习算法不同,OPS-DeMo 利用在初始学习阶段之后训练的模型。为了评估的目的,我们排除了主动学习组件,假设一组可能的对手策略变化不频繁。使用的响应策略使用 PPO 等技术进行预先训练。值得注意的是,BPR+ 和 DPN-BPR+ 等模型被排除在比较之外,因为它们不适用于连续环境。此外,SAM 也被省略,因为它没有定义的衰减参数和策略定义的歧义。
4.1 实现
实验设置涉及 2 个捕食者、2 个猎物的配置,具有完全可观察的环境状态和动作。不允许智能体之间进行直接通信。这种设置适应了每个智能体的不同策略,使不同的最佳响应策略适用于不同的对手策略。奖励在整个片段中故意保持稀疏,以最大限度地减少有关对手策略的信息。该智能体不是假设对手行为的最佳性,而是专注于根据其对对手可能行为的理解来确定最佳行为。实验是在一台配备 Apple Silicon M2 处理器和 8GB 主内存的机器上进行的。
4.2 环境设置
该设置涉及一个捕食者-猎物网格世界环境,其中包含两个捕食者和两个猎物。游戏的目标是让每个捕食者同时捕获一个猎物,目标是在最短时间内捕获两个猎物。这种方法旨在最大化在单个片段中获得的奖励。对于每个捕食者未能捕获猎物或与其他捕食者发生碰撞的每个时间步长,都会产生负奖励。这种设置解决了双重目标:优化成功的捕获并最大限度地减少不希望发生的事件。
游戏设置包括两个猎物,分别指定为「猎物 X」和「猎物 Y」,它们在环境中随机移动,仅依赖于观察结果。第一个捕食者被称为「捕食者 A」,第二个被称为「捕食者 B」。类似地,猎物是「猎物 X」和「猎物 Y」。捕食者 B 有两种可能的策略:追捕猎物 X 或猎物 Y. ��并定期切换。捕食者 A 适应这些变化,根据其信念选择最佳行为。✅
在两个捕食者的训练环境中,奖励结构定义如下:捕获两个猎物 +100,每个时间步长没有相邻猎物 -1,与智能体碰撞 -1。主要目标是最大化捕食者 A 的奖励,并准确更新关于捕食者 B 当前策略的信念。在图 2 中,我们提供了一个视觉表示来说明所描述的捕食者-猎物场景。

[图片:捕食者-猎物环境图]
4.3 训练设置
我们的训练环境是一个 10 × 10 的捕食者-猎物网格世界,使用 OpenAI Gym 库 [33] 创建。在这个网格世界中,每个训练片段持续最长 40 个时间步长。为了促进训练过程,我们使用 Stable-Baselines3 库 [34]。具体来说,我们训练了捕食者 B 的两种潜在策略,重点是追捕猎物 A 或猎物 B. ��这种训练利用 PPO 算法,并运行了最多 1,000,000 次迭代。为了解决稀疏奖励问题,我们在环境提供的奖励中引入了基于捕食者 B 与其目标猎物之间曼哈顿距离的惩罚。随后,我们继续使用 PPO 算法为捕食者 B 的每种潜在策略训练捕食者 A 的响应策略,再次达到 1,000,000 次迭代。✅
4.4 策略切换的模拟
在将训练好的模型部署到环境中后,我们对捕食者 B 实施了在追捕猎物 X 和猎物 Y 之间的周期性策略切换。至关重要的是,关于捕食者 B 当前策略的信息对捕食者 A 保持隐藏。捕食者 A 只能访问关于其自身奖励和捕食者 B 在每个时间步长选择的动作的信息。捕食者 B 利用在线数据来计算观察到的误差和马尔可夫状态的相应衰减,更新运行误差。然后根据此信息从其策略库中选择捕食者 B 的响应策略,以确定其在下一个时间步长的动作。
4.5 与实验相关的超参数
除其他外,我们希望关注我们在工作中进行过实验的以下超参数:
- 尝试不同的严格性系数:我们使用不同的严格性系数 α ∈ {0.8, 0.9, 0.95, 0.99} 进行实验,以评估它们对模型性能的影响。数据收集在假设策略与对手的隐藏策略一致的时间步长上。
- 尝试独立的 PPO 训练模型:为了比较 OPS-DeMo 与 PPO 的性能,我们使用 PPO 训练了一个捕食者 A 模型。在此设置中,捕食者 B 每 100 个时间戳切换一次策略,训练持续最多 1,000,000 次迭代。然后评估这些训练好的模型,并使用累积奖励比较它们的性能。独立的 PPO 训练模型没有用于预测对手行为的信念机制,仅使用环境状态来确定其下一个动作。
现在,我们提供一些实证结果来分析我们解决方案的新颖性和效率。
4.6 运行误差估计的性能
我们评估了 OPS-DeMo 的运行误差估计方法在捕食者 B 每 n 个时间步长切换策略时的有效性。
在图 3 和图 4 中,很明显,当假设的策略正确时,运行误差保持较低,并且当假设的策略不正确时,运行误差保持在阈值。值得注意的是,在策略切换点,不正确假设的策略的运行误差迅速增加,而正确策略的运行误差下降相对较慢。这是因为当对手遵循假设对手策略 (AOP) 时,误差衰减更接近于预期的观察误差,而当对手不遵循 AOP 时,观察到的误差远大于衰减。在检测到切换后,对新假设的策略的运行误差进行减半,有助于正确假设的运行误差快速收敛到较低的值。

[图片:捕食者 B 的两种可能策略的运行误差,基于捕食者 A 的观察结果,捕食者 B 每 100 个时间步长切换一次策略]

[图片:捕食者 B 的两种可能策略的运行误差,基于捕食者 A 的观察结果,捕食者 B 每 200 个时间步长切换一次策略]
4.7 严格性系数的影响
我们在捕食者-猎物环境中的实验涉及在捕食者 B 每 100 个时间步长切换策略时改变严格性系数 (α)。我们检查了运行误差在不同严格性条件下的行为。

图 5 说明了严格性系数的增加会导致对手策略切换后运行误差更快地上升。然而,它也表明,在过渡到该特定 AOP 后,运行误差的降低在更高的严格性条件下更加缓慢。这种现象发生是因为当对手遵循 AOP 时,添加到运行误差中的分量通常为负,而当对手偏离 AOP 时,则为正。衰减越接近遵循 AOP 时的预期观察误差(公式 5),负值的幅度就越小,正值的幅度就越大。
4.8 假设对手策略的准确性
在我们的实验中,我们在捕食者 B 每 100 个时间步长切换策略时改变了严格性系数 (α)。我们通过计算假设策略与实际策略匹配的时间步长与总时间步长之比来评估 AOP 的准确性。

图 6 说明了随着我们增加严格性系数,准确性会提高。这表明误差估计方法变得不那么宽松,在区分一些类似但不同的策略方面变得更有识别力。这是因为更高的严格性系数会使运行误差更快地上升,并更早地检测到策略切换。但在权衡中,来自环境的自然噪声在这种情况下可能会产生一些误报。

[图片:基于捕食者 A 的观察结果,捕食者 B 的假设对手策略 (AOP) 的准确性。捕食者 B 每 100 个时间步长切换一次策略,显示了不同严格性系数对准确性的影响]
4.9 通过片段累积奖励进行比较
基于包含 25 次运行的实验数据,每次运行持续 1000 个片段,可以明显看出每个片段的累积奖励有所提高。这些改进源于两个捕食者之间协作动态的增强。捕食者 A 对捕食者 B 的策略切换表现出快速适应性,根据其推断的关于捕食者 B 当前策略的信念制定响应。
在图 7 中,我们观察到,虽然独立的 PPO 训练模型在大多数片段中表现良好,但也有一些情况下,它未能在定义的 40 个时间步长内捕获两个猎物。因此,由于缺乏协作努力,它错过了 +100 的奖励。相反,OPS-DeMo 在运行时动态地检测到捕食者 B 的策略,并相应地调整其响应策略,表现出这种失败的发生次数更少。

图 8 说明了 OPS-DeMo 在捕食者 A 的平均片段奖励方面比独立的 PPO 训练模型提高了 49.6%。这种改进归因于 OPS-DeMo 在处理由于对捕食者 B 当前策略的高度不确定性而导致的方差增加方面的鲁棒性。
表 1 片段累积奖励的统计摘要
| 算法 | 平均值 | 标准差 |
|---|---|---|
| OPS-DeMo + PPO | 89.9662 | 18.7922 |
| PPO | 60.1371 | 53.0235 |
在表 1 中观察到的 OPS-DeMo 奖励的一致性(如较低的标准差所示)源于对捕食者 B 行为的确定性增加。OPS-DeMo 根据这种确定性做出明智的决策,与独立的 PPO 训练模型形成对比,后者往往会忽略捕食者 B 的最近动作数据。
结论与未来工作
在非平稳的多智能体环境中检测策略切换具有挑战性,但有利可图。当动作分布均匀或数据有限时,很难检查遵守情况。使用比较观察到的动作和预期动作的误差指标有助于解决这个问题,而衰减机制可以防止误差升级。对可能策略的运行误差计算有助于推断切换,从而能够选择适当的响应策略。所提出的 OPS-DeMo 算法使用这些方法进行检测和响应,在每个片段的累积奖励方面优于独立的 PPO 模型,并且标准差更低。在未来,我们计划在以下方面开展工作:
- 结合连续学习以更精确地估计对手策略。
- 开发一种鲁棒的方法来检测具有均匀动作频率分布的对手策略,以及检测和学习不可预见的对手策略。
参考文献
- [1] Russell, S. J., & Norvig, P. (2016). ✅Artificial intelligence: a modern approach. Pearson Education.
- [2] Liao, X. , & Zhang, H. (2019). Deep reinforcement learning for autonomous driving: A survey. ✅IEEE/CAA Journal of Automatica Sinica, 6(6), 1023-1038.
- [3] Shoham, Y. , & Leyton-Brown, K. (2009). ✅Multiagent systems: Algorithmic, game-theoretic, and logical foundations. Cambridge University Press.
- [4] Sutton, R. S., & Barto, A. G. (2018). ✅Reinforcement learning: An introduction. MIT press.
- [5] Bowling, M. , & Veloso, M. (2002). Multiagent learning using a Bayesian approach. ✅Artificial Intelligence, 136(2), 215-250.
- [6] Tuyls, K. , & Nowe, A. (2005). A bayesian approach to multiagent learning in dynamic environments. ✅Journal of Artificial Intelligence Research, 23, 295-320.
- [7] Foerster, J. N., Zhang, T., & Whiteson, S. (2018). Learning with opponent-learning awareness. ✅arXiv preprint arXiv:1802.09631.
- [8] Liu, S. , et al. (2020). Meta-learning for multi-agent reinforcement learning. ✅arXiv preprint arXiv:2005.02978.
- [9] Lillicrap, T. P., et al. (2015). Continuous control with deep reinforcement learning. ✅arXiv preprint arXiv:1509.02971.
- [10] Littman, M. L. (1994). Markov games as a framework for multi-agent reinforcement learning. ✅Machine learning, 18(1), 121-153.
- [11] Busoniu, L. , Babuska, R., De Schutter, B., & Narendra, K. S. (2010). ✅Multi-agent reinforcement learning: An overview. In Adaptive and learning agents and multi-agent systems (pp. 1-15). Springer, Berlin, Heidelberg.
- [12] Watkins, C. J. C. H. (1989). ✅Learning from delayed rewards. PhD thesis, King’s College, Cambridge.
- [13] Minsky, M. (1961). ✅Steps toward artificial intelligence. Proceedings of the IRE, 49(1), 8-30.
- [14] Lowe, R. , et al. (2017). Multi-agent deep reinforcement learning from decentralized observations. ✅arXiv preprint arXiv:1703.02752.
- [15] Williams, R. J. (1992). Simple statistical gradient-following algorithms for connectionist reinforcement learning. ✅Machine learning, 8(3-4), 229-256.
- [16] Mnih, V. , et al. (2013). Playing Atari with deep reinforcement learning. ✅arXiv preprint arXiv:1312.5602.
- [17] Mnih, V. , et al. (2016). Asynchronous methods for deep reinforcement learning. ✅arXiv preprint arXiv:1602.01783.
- [18] Haarnoja, T. , et al. (2018). Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. ✅arXiv preprint arXiv:1801.01290.
- [19] Schulman, J. , et al. (2015). Trust region policy optimization. ✅arXiv preprint arXiv:1502.05477.
- [20] Schulman, J. , et al. (2017). Proximal policy optimization algorithms. ✅arXiv preprint arXiv:1707.06347.
- [21] Kraus, S. , & S. (2015). ✅Learning in multiagent systems. MIT press.
- [22] Littman, M. L. (1996). Learning successful list-length bounds in the list-length domain. ✅Machine learning, 22(1-3), 27-45.
- [23] Singh, S. P., Jaakkola, T., & Littman, M. L. (2000). Convergence results for single-agent reinforcement learning with function approximation. ✅In Proceedings of the 17th International Conference on Machine Learning (ICML) (pp. 708-715).
- [24] Littman, M. L. (2000). The corridor problem: A case study in reinforcement learning. ✅Machine learning, 38(1-3), 109-133.
- [25] Strehl, A. L., Li, L., & Littman, M. L. (2006). Reinforcement learning in the presence of unknown transition dynamics. ✅In Proceedings of the 23rd International Conference on Machine Learning (ICML) (pp. 881-888).
- [26] Finn, C. , Abbeel, P., & Levine, S. (2017). Model-agnostic meta-learning for fast adaptation of deep networks. ✅arXiv preprint arXiv:1703.03400.
- [27] Foerster, J. N., et al. (2017). Learning to cooperate by learning to compete. ✅arXiv preprint arXiv:1706.02275.
- [28] Sukhbaatar, S. , et al. (2016). Learning multiagent communication with backpropagation. ✅arXiv preprint arXiv:1605.07139.
- [29] Rashid, T. , et al. (2018). Deep reinforcement learning for tabular multiagent games. ✅arXiv preprint arXiv:1803.01492.
- [30] Lowe, R. , et al. (2017). Multi-agent deep reinforcement learning from decentralized observations. ✅arXiv preprint arXiv:1703.02752.
- [31] Son, K. , et al. (2019). Deep policy iteration for multi-agent reinforcement learning. ✅arXiv preprint arXiv:1906.00808.
- [32] Haque, M. M., et al. (2020). A switching agent model for adaptive opponent policy detection in multi-agent reinforcement learning. ✅arXiv preprint arXiv:2006.00357.
- [33] Brockman, G. , et al. (2016). OpenAI Gym. ✅arXiv preprint arXiv:1606.01540.
- [34] Stable Baselines3. (2020). https://stable-baselines3.readthedocs.io/en/master/
Q: 这篇论文试图解决什么问题?
A: 这篇论文试图解决的问题是在多智能体强化学习(Multi-agent Reinforcement Learning, MARL)环境中,如何准确感知对手策略的问题。特别是在动态环境中,对手可能突然改变他们的策略,这给智能体的学习和适应带来了挑战。论文指出,现有的MARL算法在处理非静态和隐藏的对手策略时存在高方差问题,导致奖励性能下降。此外,现有方法还面临智能体间通信需求、对显式奖励信息的依赖、高计算需求和采样效率低下等挑战。
为了解决这些问题,论文提出了一个名为OPS-DeMo(Online Policy Switch-Detection Model)的在线算法。该算法使用动态误差衰减来检测对手策略的变化,并能实时更新其对对手策略的信念,从而从预训练的响应策略库中选择相应的响应。这样,即使在对手策略发生突然变化的情况下,也能提高智能体的适应性和决策的准确性。
Q: 有哪些相关研究?
A: 论文中提到了多个与多智能体强化学习(MARL)相关的研究工作,以下是一些主要的相关研究:
- Proximal Policy Optimization (PPO) [20]: 一种策略梯度方法,用于优化连续控制环境中的代理策略。
- Actor-Critic with Experience Replay (ACER): 结合了经验回放机制的Actor-Critic方法,用于提高学习效率。
- Trust Region Policy Optimization (TRPO): 一种策略优化方法,通过信任域来限制策略更新的步长。
- Deep Deterministic Policy Gradient (DDPG): 一种用于连续动作空间的深度强化学习算法。
- BPR+ [5] 和 DPN-BPR+ [6]: 这两种算法都旨在处理非静态环境中的对手策略变化,通过假设对手策略在多个静态策略之间切换。
- LOLA [7]: 旨在影响对手行为的算法,通过学习如何塑造对手的学习过程来获得优势。
- Meta-MAPG [8]: 一种基于元学习的算法,用于连续适应环境动态变化。
- MDP-CL [24], DriftER [25], 和 RL-CD [22], QCD [23]: 这些算法设计用来处理非静态对手,通过假设对手定期在多个静态策略之间切换。
- MADDPG [14]: 一种多智能体深度确定性策略梯度算法,用于学习有效的多智能体策略。
- REINFORCE [15], DQN [16], AAC [17], SAC [18], TRPO [19]: 这些是针对单智能体强化学习任务的算法,使用不同的技术和方法,如价值迭代、策略迭代、Q学习和策略梯度方法。
- DRON [29], MADDPG [30], DPIQN [31]: 这些是针对多智能体系统的深度强化学习算法,通过学习对手的行为特征来适应非静态环境。
- SAM [32]: 一个结合了DDPG和对手建模的算法,用于适应性地调整响应策略。
这些研究工作为论文提出的OPS-DeMo算法提供了理论和技术背景,同时也展示了在多智能体环境中处理动态对手策略的现有挑战和方法。论文通过比较和分析这些相关工作,提出了自己的创新点和解决方案。
Q: 论文如何解决这个问题?
A: 论文提出了一个名为OPS-DeMo(Online Policy Switch-Detection Model)的在线算法来解决在多智能体环境中准确检测对手策略变化的问题。以下是该算法解决这个问题的关键步骤和方法:
- 运行误差估计(Running Error Estimation):
- 引入一个新的度量标准来衡量代理与策略的一致性,该标准基于代理最近的行动,并实时比较观察到的行动与预期的概率。
- 动态误差衰减(Dynamic Error Decay):
- 实现一个衰减机制,以防止由于策略固有的随机性导致的错误累积。这个衰减机制考虑了代理遵循策略时的预期误差以及不遵循策略时的预期误差。
- 假设对手策略(Assumed Opponent Policy, AOP)银行:
- 维护一个包含可能的对手策略的银行,并使用这个银行来计算对手选择特定行动的概率。
- 预训练的响应策略银行(Pre-Trained Response Policy Bank):
- 对于AOP银行中的每个对手策略,训练一个响应策略,以便在多智能体环境中有效使用,如PPO算法。
- 在线策略切换检测:
- 当前假设的对手策略的运行误差超过阈值时,检测到策略切换,并选择新的假设对手策略,该策略具有最低的运行误差。
- 适应性响应策略选择:
- 根据更新的信念关于对手当前策略,从预训练的响应策略银行中选择适当的响应策略,以最大化累积奖励。
- 算法优化:
- 为了适应边缘设备的资源限制,优化策略切换检测机制,使其能够在严格的资源限制下运行,并能够即时处理观察结果,无需存储。
- 实验评估:
- 在Predator-Prey设置等动态场景中,通过比较评估,展示了OPS-DeMo方法相较于PPO训练模型在处理突然策略变化时的优越性能。
通过这些方法,OPS-DeMo算法能够实时检测对手策略的变化,并迅速调整其响应策略,从而在多智能体环境中实现更加稳健和有效的决策。
Q: 论文做了哪些实验?
A: 论文中进行了一系列的实验来评估OPS-DeMo算法的性能。以下是实验的主要方面:
- 实验设置:
- 使用了一个2个捕食者和2个猎物的配置,环境状态和行动都是完全可观察的。没有直接的智能体间通信。
- 环境配置:
- 实验在一个Predator-Prey的网格世界环境中进行,目标是每个捕食者尽可能快地捕捉到一个猎物。
- 训练设置:
- 使用OpenAI Gym库创建了一个10×10的捕食者-猎物网格世界。训练使用了Stable-Baselines3库,并针对Predator B训练了两种可能的策略。
- 策略切换模拟:
- 在环境中部署训练好的模型后,对Predator B实施了定期的策略切换,而Predator A则不知道Predator B当前的策略。
- 超参数实验:
- 进行了不同严格性因子(α)的实验,以评估它们对模型性能的影响。同时,将OPS-DeMo与单独使用PPO训练的模型进行了比较。
- 运行误差估计性能:
- 评估了OPS-DeMo的运行误差估计方法在Predator B定期切换策略时的有效性。
- 严格性因子的影响:
- 通过改变严格性因子,研究了它对运行误差的影响。
- 假设对手策略的准确性:
- 通过计算假设策略与实际策略匹配的比率,评估了AOP的准确性。
- 累积奖励的比较:
- 通过25次运行,每次1000个episode的数据,比较了OPS-DeMo和单独使用PPO训练的模型在累积奖励方面的表现。
- 统计总结:
- 提供了OPS-DeMo和PPO模型在累积奖励方面的统计摘要,包括平均值和标准差。
这些实验结果表明,OPS-DeMo在处理对手策略变化时具有更高的适应性和鲁棒性,能够实现更一致的奖励,并在多智能体环境中做出更有效的决策。
Q: 有什么可以进一步探索的点?
A: 论文在结论部分提出了一些未来工作的方向,这些可以作为进一步探索的点:
- 持续学习(Continuous Learning): 论文提出计划在未来的工作中引入持续学习机制,以实现更精确的对手策略估计。
- 检测具有均匀频率分布行动的对手策略: 对于那些行动分布均匀的对手策略,检测其策略变化可能更加困难。论文提出需要开发更健壮的方法来检测这类对手的策略。
- 学习和适应未知对手策略: 在实际应用中,智能体可能会遇到之前未见过的对手策略。论文提出需要进一步研究如何让智能体能够检测并学习应对这些未知策略。
- 算法优化: 虽然论文中已经对OPS-DeMo进行了一些优化,以适应资源受限的环境,但仍有进一步优化算法的空间,以提高其在更广泛环境下的适用性和效率。
- 更广泛的环境和任务测试: 论文中的实验主要在一个Predator-Prey的网格世界环境中进行。未来的工作可以在更广泛的环境和任务中测试OPS-DeMo的性能,以验证其泛化能力。
- 多智能体系统中的合作与竞争: 论文中提到了多智能体系统中的合作与竞争行为,未来的研究可以更深入地探索如何在这些复杂的交互中实现更有效的策略学习和适应。
- 实际应用: 将OPS-DeMo算法应用于现实世界的问题,如自动驾驶车辆的交互、机器人团队协作等,这可能需要对算法进行调整以适应特定的应用场景。
- 算法的可解释性和透明度: 提高算法的可解释性,使得智能体的决策过程更加透明,这有助于增强人类对智能体行为的信任。
- 对手建模的改进: 进一步改进对手建模技术,以便更准确地预测和适应对手的行为变化。
- 多模态学习: 探索多模态学习方法,结合不同类型的数据(如视觉、语言、行为数据)来提高策略学习和适应的能力。
这些探索点可以帮助研究者们扩展和深化对多智能体强化学习领域中策略检测和适应问题的理解。
Q: 总结一下论文的主要内容
A: 这篇论文的主要内容可以概括为以下几个要点:
- 问题背景: 论文讨论了在多智能体强化学习(MARL)环境中,智能体准确感知对手策略的重要性,尤其是在动态环境中,对手策略可能突然变化,给智能体的学习和适应带来挑战。
- 现有挑战: 指出现有MARL算法在处理非静态和隐藏的对手策略时存在高方差问题,导致奖励性能下降,并面临通信需求、计算需求和采样效率等挑战。
- OPS-DeMo算法: 提出了一个名为OPS-DeMo的在线算法,使用动态误差衰减来检测对手策略的变化,并从预训练的响应策略库中选择相应的响应。
- 运行误差估计: 引入了一个新的度量标准,用于在线评估智能体与策略的一致性,仅使用观察到的状态-行动对。
- 动态误差衰减机制: 为了解决策略固有随机性导致的错误累积问题,实现了一个衰减机制,考虑了遵循和偏离策略时的预期误差。
- 实验评估: 通过在Predator-Prey环境中的实验,比较了OPS-DeMo算法与现有算法(如PPO)的性能,展示了OPS-DeMo在处理策略突然变化时的有效性和鲁棒性。
- 未来工作: 提出了未来研究的方向,包括持续学习、检测具有均匀频率分布行动的对手策略、学习和适应未知对手策略等。
- 结论: OPS-DeMo算法能够有效地检测对手策略的切换,并通过选择适当的响应策略来提高智能体在多智能体环境中的表现。
论文通过提出OPS-DeMo算法,为多智能体环境中的策略检测和适应问题提供了一种新的解决方案,并通过对比其他现有方法,证明了其有效性。同时,论文也为未来的研究提供了一些有价值的方向。